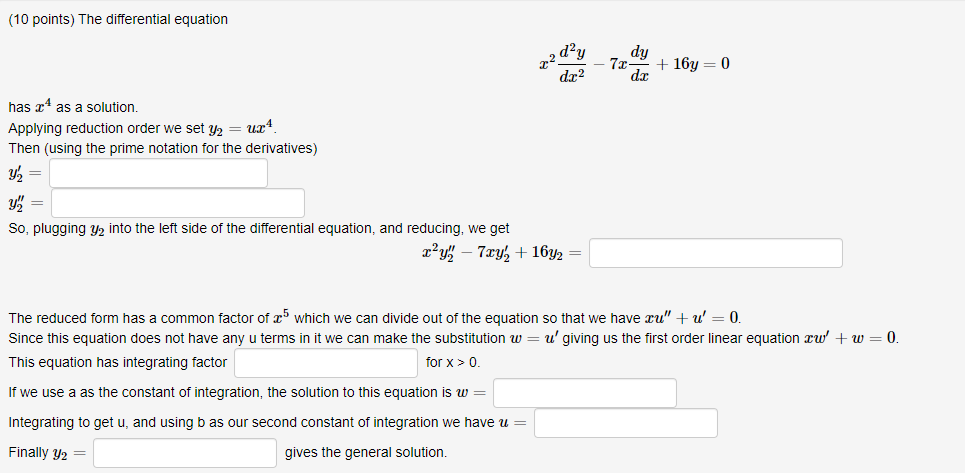
(10 points) The differential equation has 4 as a solution. Applying reduction order we set y = ux4. Then (using the prime notation for the derivatives) Y = Y" = So, plugging y into the left side of the differential equation, and reducing, we get xdy dx dy 7x- +16y=0 dx xy - 7xy + 16y2 = u' giving us the first order linear equation xw' + w = 0. The reduced form has a common factor of 25 which we can divide out of the equation so that we have xu" + u' = 0. Since this equation does not have any u terms in it we can make the substitution w This equation has integrating factor for x > 0. If we use a as the constant of integration, the solution to this equation is w = Integrating to get u, and using b as our second constant of integration we have u = = Finally Y2 gives the general solution.