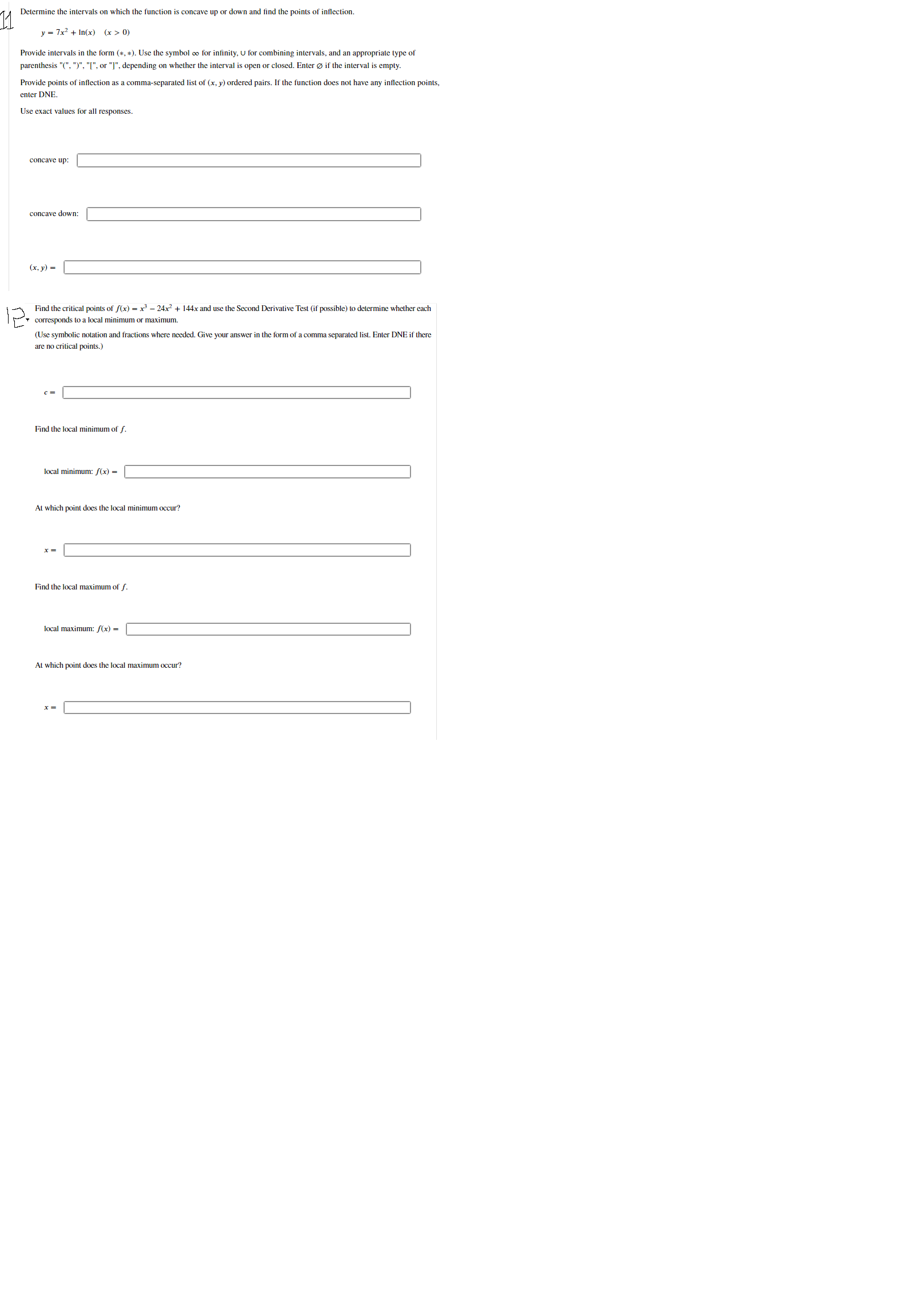
11 Determine the intervals on which the function is concave up or down and find the points of inflection. y = 7x + In(x) (x > 0) Provide intervals in the form (*,*). Use the symbol oo for infinity, U for combining intervals, and an appropriate type of parenthesis "(", ")", "[", or "]", depending on whether the interval is open or closed. Enter if the interval is empty. Provide points of inflection as a comma-separated list of (x, y) ordered pairs. If the function does not have any inflection points, enter DNE. Use exact values for all responses. concave up: concave down: (x, y) = Find the critical points of f(x) = x- 24x + 144x and use the Second Derivative Test (if possible) to determine whether each corresponds to a local minimum or maximum. (Use symbolic notation and fractions where needed. Give your answer in the form of a comma separated list. Enter DNE if there are no critical points.) Find the local minimum of f. local minimum: f(x) = At which point does the local minimum occur? x = Find the local maximum of f. local maximum: f(x) = At which point does the local maximum occur?