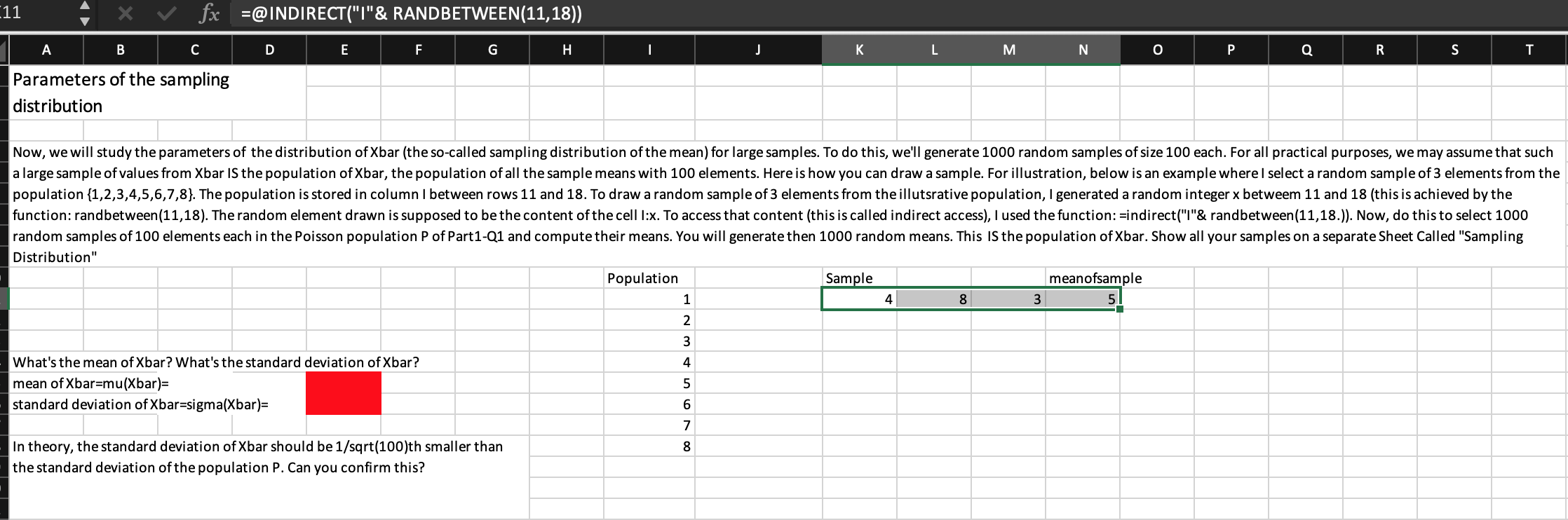
11 fx =@INDIRECT("/"& RANDBETWEEN(11,18)) B C D E F G H I J L M N o Q R S T Parameters of the sampling distribution Now, we will study the parameters of the distribution of Xbar (the so-called sampling distribution of the mean) for large samples. To do this, we'll generate 1000 random samples of size 100 each. For all practical purposes, we may assume that such a large sample of values from Xbar IS the population of Xbar, the population of all the sample means with 100 elements. Here is how you can draw a sample. For illustration, below is an example where I select a random sample of 3 elements from the population {1,2,3,4,5,6,7,8}. The population is stored in column I between rows 11 and 18. To draw a random sample of 3 elements from the illutsrative population, generated a random integer x betweem 11 and 18 (this is achieved by the function: randbetween(11,18). The random element drawn is supposed to be the content of the cell 1:x. To access that content (this is called indirect access), I used the function:=indirect("1"& randbetween(11,18.)). Now, do this to select 1000 random samples of 100 elements each in the Poisson population P of Part1-Q1 and compute their means. You will generate then 1000 random means. This is the population of Xbar. Show all your samples on a separate Sheet Called "Sampling Distribution" Population Sample meanofsample 1 4 8 3 5 2 W NP What's the mean of Xbar? What's the standard deviation of Xbar? mean of Xbar=mu(Xbar)= standard deviation of Xbar=sigma(Xbar)= 4 5 6 7 8 In theory, the standard deviation of Xbar should be 1/sqrt(100)th smaller than the standard deviation of the population P. Can you confirm this? 11 fx =@INDIRECT("/"& RANDBETWEEN(11,18)) B C D E F G H I J L M N o Q R S T Parameters of the sampling distribution Now, we will study the parameters of the distribution of Xbar (the so-called sampling distribution of the mean) for large samples. To do this, we'll generate 1000 random samples of size 100 each. For all practical purposes, we may assume that such a large sample of values from Xbar IS the population of Xbar, the population of all the sample means with 100 elements. Here is how you can draw a sample. For illustration, below is an example where I select a random sample of 3 elements from the population {1,2,3,4,5,6,7,8}. The population is stored in column I between rows 11 and 18. To draw a random sample of 3 elements from the illutsrative population, generated a random integer x betweem 11 and 18 (this is achieved by the function: randbetween(11,18). The random element drawn is supposed to be the content of the cell 1:x. To access that content (this is called indirect access), I used the function:=indirect("1"& randbetween(11,18.)). Now, do this to select 1000 random samples of 100 elements each in the Poisson population P of Part1-Q1 and compute their means. You will generate then 1000 random means. This is the population of Xbar. Show all your samples on a separate Sheet Called "Sampling Distribution" Population Sample meanofsample 1 4 8 3 5 2 W NP What's the mean of Xbar? What's the standard deviation of Xbar? mean of Xbar=mu(Xbar)= standard deviation of Xbar=sigma(Xbar)= 4 5 6 7 8 In theory, the standard deviation of Xbar should be 1/sqrt(100)th smaller than the standard deviation of the population P. Can you confirm this