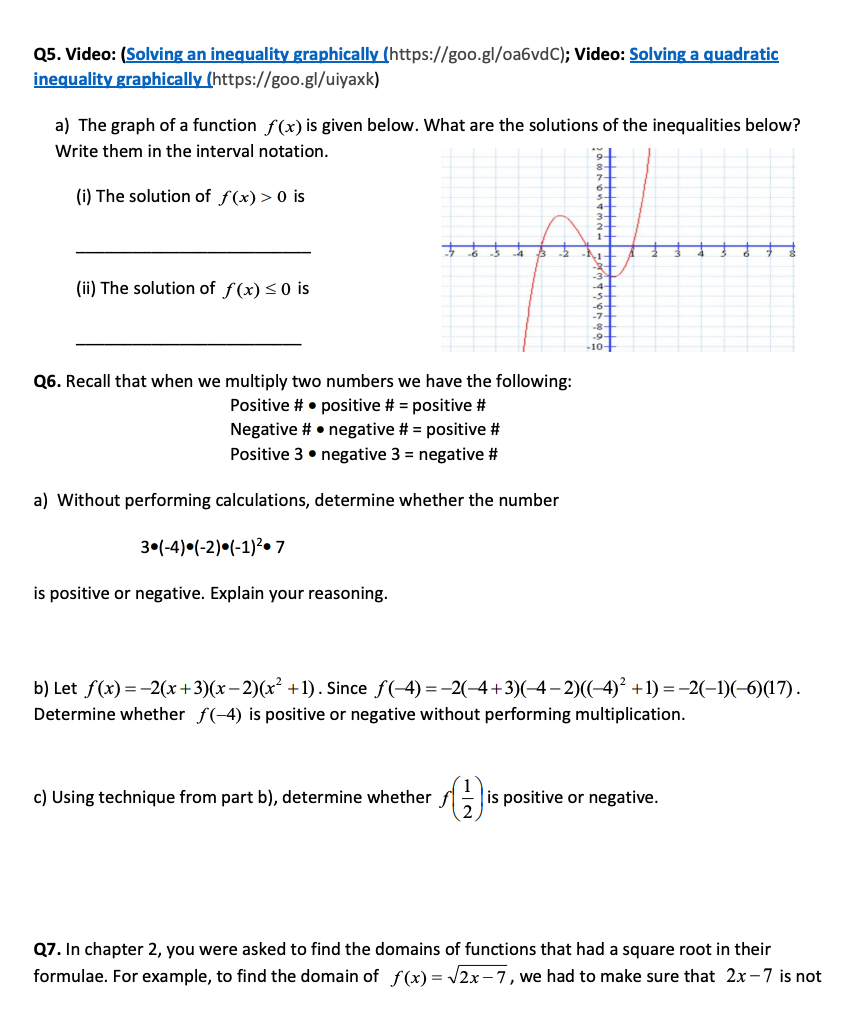
(11. Video: Behavior ofa rational function!httpsyoutubegMimVBkgVSle a] Explain in your own words the meaning of the following symbols: x>q' y)oo Explore the behavior of points on the graph of f(x) = when x ) 2'. Go to https:[[www.desmos.com[calculatorcvggBlygBm and, using the slider, move the point on the graph. Note the coordinates of the point. Write your conclusions below: As .1: > 23 yvalues . The points on the graph comes closer and closer to the line b} Repeat similar analysis when x is greaterthan 2. You will need the following notation: x > (1" means x values approach q from the right or through values that are greater than q x > +00 means that x values increase without bound, that is they can be arbitrarily large. {i} Use a calculator to complete the table: y 5 x = {ii} In your own words, describe the x 2 2.1 behavior of x values: 2.01 2.001 {iii} Use symbols to describe behavior of x: x > 230,01 2.00001 [iv] In your own words, describe the behavior ofy values: [v] Use symbols to describe behavior of y: y > [vi] Summarize the ndings in a sentence: as x > then y > (vii) Use the table of values to plot the points on the graph of f(x) Describe how the points on the graph behave when x -> 2 Q2. Draw a graph of a function that has given properties. First example was done for you. a) When x -> 2" then y -> too and b) When x -> 2" then y -> too and when x - 2* then y -> too. when x -> 2* then y -> co. Q3. Consider function f(x) = - 5x x+1 . Now, you will investigate what happens to values f(x) when x -> too and x -> -co . a) Complete the table. Use a calculator; write the decimal until first nonzero digit X 5x X 5x x+1 x+1 10 -10 100 -100 1000 -1000 10,000 -10,000 100,000 -100,000b) Write your conclusions using the arrow notation. When x -> too then y -> When x -> co then y-> c) Plot the points in the coordinate system below. Write down your observations: When x -> too, the points on the graph When x -> co, the points on the graph Q4. a) Use the graph to complete the statements below When x- -3- then y - When x - -3+ then y - When x - 3- then y - When x - 3+ then y - When x - -00 then y - When x - +co then y - b) A horizontal line y=a is a horizontal asymptote for f(x) if y -> a when x -> too or when x-> -00 Does the graph above have a horizontal asymptote? If yes, what is its equation? c) A vertical line x = a is a vertical asymptote for f(x) if y -> too or -co when x -> a* orx -> a Does the graph above have a vertical asymptote(s)? If yes, what is its equation?(15. Video: [Solving an inegual'm: graphicalm Ihttps:lfgoo.glfoa6vdc); Video: Solving a Quadratic ingual' graphically; lhttps:goo.glfuiyaxk} a} The graph of a function f(x} is given below. What are the solutions of the inequalities below? Write them in the interval notation. {i} The solution of f(x) 5 0 is 9 E 1' 6 5 I' 3 2 I (ii) The solution of f(x) 5 0 is Q6. Recall that when we multiply two numbers we have the following: Positive ii a positive ii = positive if Negative ii I negative ii = positive if Positive 3 0 negative 3 = negative if a] Without performing calculations, determine whether the number 3-H}(-2)-{-1)2 7 is positive or negative. Explain your reasoning. b] Let f(x) = 2(x +3}(x 2m:2 +1) . Since f(4) = 2(4+3}(4 2}((4)2 +1) = 2(l}(6)(17) . Determine whether f(4) is positive or negative without performing multiplication. c) Using technique from part b), determine whether [ii] is positive or negative. Q7. In chapter 2, you were asked to find the domains of functions that had a square root in their formulae. For example, to nd the domain of f(x) = ax7 , we had to make sure that 2x'l' is not negative, as square root ofa negative number is not a real number. So, to nd the domain we had to solve the inequality 2.: -7 2 0. Write an appropriate inequality that should be used to find the domains of functions below. Do not solve. a} f(x) = J23:3 5x2 3x 3: must satisfythe inequality: b} 3(3) = 3: +1 it must satisfy the inequality