#12

Find the standarddeviation, s, of sample data summarized in the frequency distribution table below by using the formulabelow, where x represents the classmidpoint, f represents the classfrequency, and n represents the total number of sample values.Also, compare the computed standard deviation to the standard deviation obtained from the original list of datavalues, 11.1.

s= Square root nfx²(fx)²

n(n1)

Interval 20-26 27-33 34-40 41-47 48-54 55-61 62-68

Frequency 1 3 4 2 8 32 31

Standard deviation=________(Round to one decimal place asneeded.)

Consider a difference of20% between two values of a standard deviation to be significant. How does this computed value compare with the given standarddeviation, 11.1?

A.

Thecomputedvalueisnotsignificantlydifferentfromthegivenvalue.

B.

Thecomputedvalueissignificantlygreaterthanthegivenvalue.

C.

Thecomputedvalueissignificantlylessthanthegivenvalue.

#13

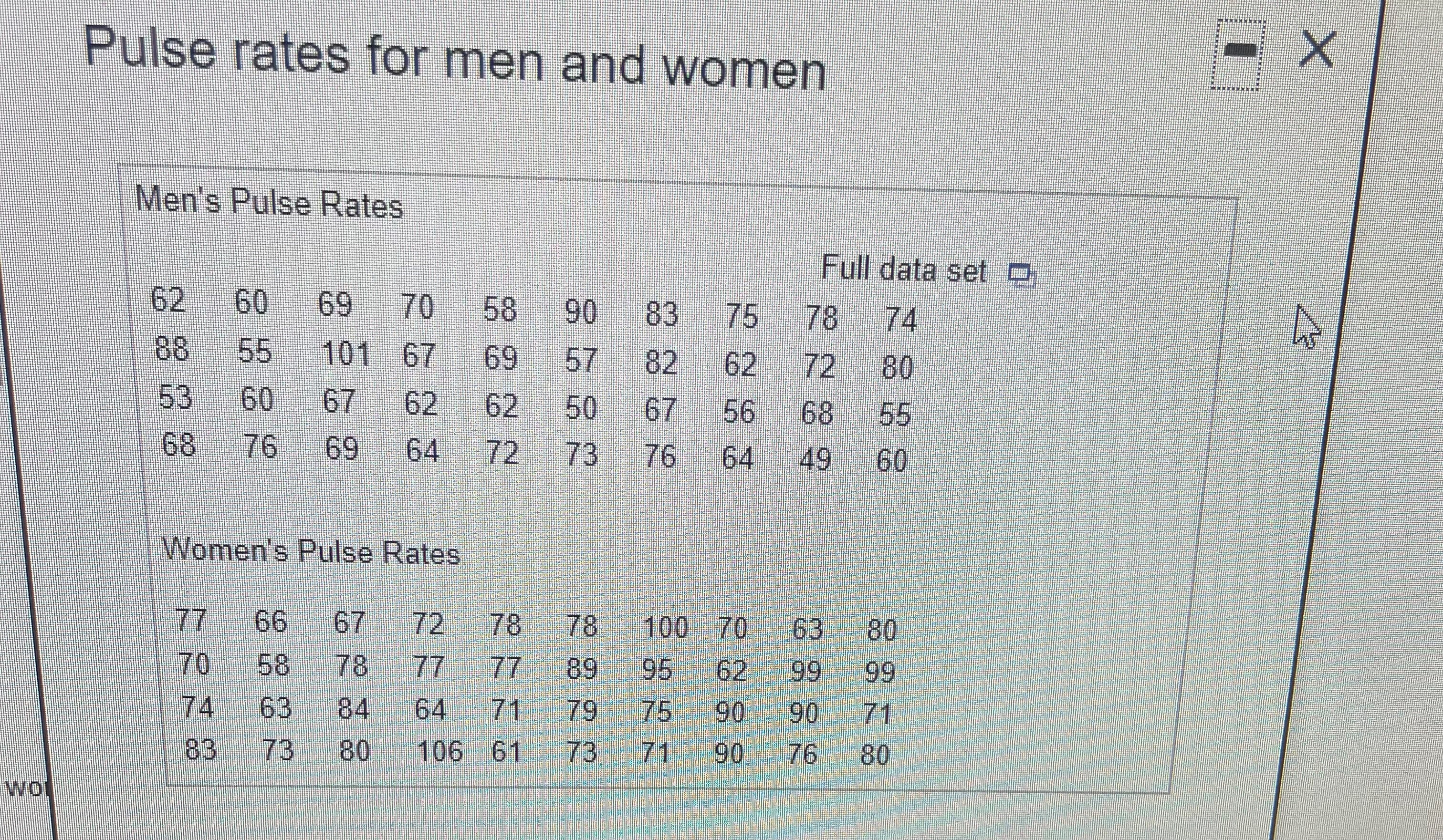
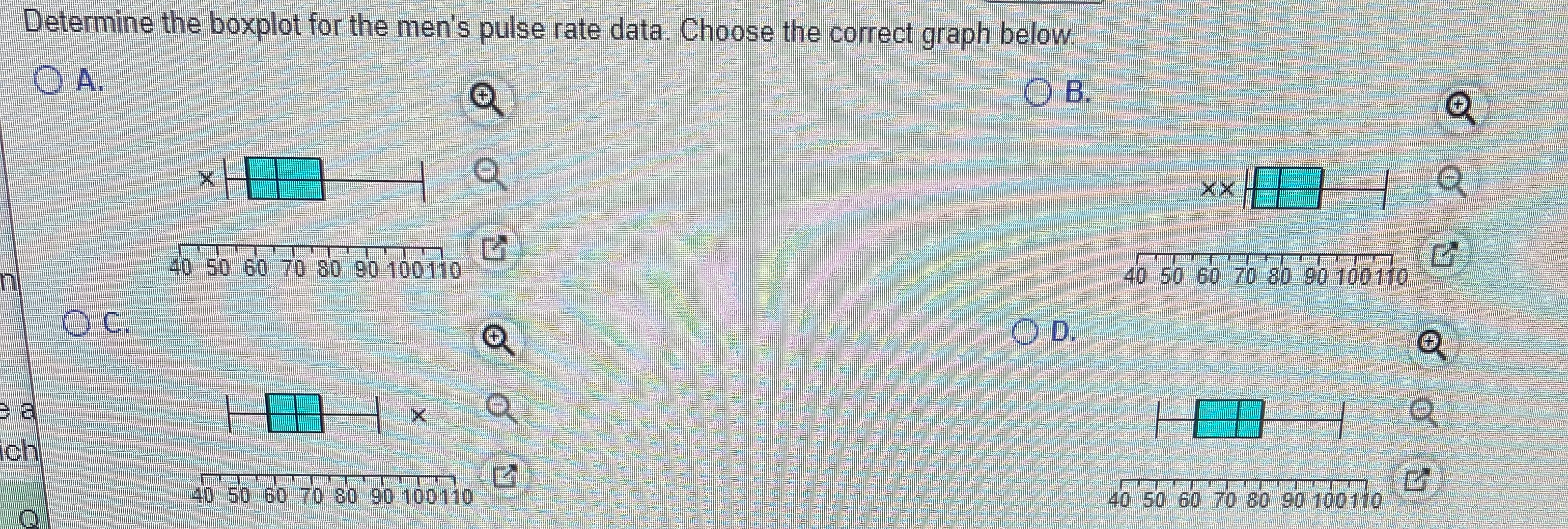
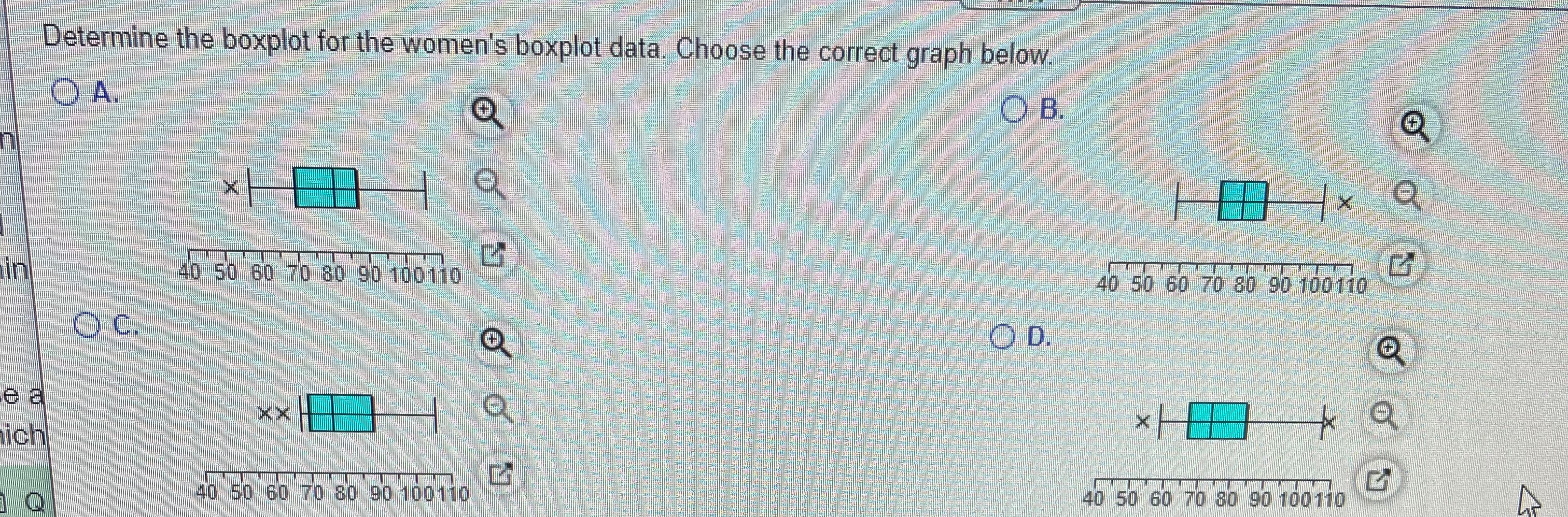
The blood platelet counts of a group of women have abell-shaped distribution with a mean of 259.6 and a standard deviation of 63.8. (All units are 1000 cells/L.) Using the empiricalrule, find each approximate percentage below.

a.

What is the approximate percentage of women with platelet counts within 2 standard deviations of themean, or between 132.0 and 387.2?

b.

What is the approximate percentage of women with platelet counts between 195.8 and 323.4?

a. Approximately _______% of women in this group have platelet counts within 2 standard deviations of themean, or between 132.0 and 387.2.

(Type an integer or a decimal. Do notround.)

b. Approximately _______% of women in this group have platelet counts between 195.8 and 323.4.

(Type an integer or a decimal. Do notround.)

#15

The boxplot shown below results from the heights(cm) of males listed in a data set. What do the numbers in that boxplot tellus?

The minimum height is _______cm, the first quartile Q1 is _______cm, the second quartile Q2 (or themedian) is ______cm, the third quartile Q3 is ______cm, and the maximum height is ______cm.

(Type integers or decimals. Do notround.)

#16

If your score on your next statistics test is converted to a zscore, which of these z scores would youprefer: 2.00, 1.00, 0, 1.00,2.00? Why?

A.

The z score of 1.00 is most preferable because it is 1.00 standard deviation above the mean and would correspond to an above average test score.

B.

The z score of 2.00 is most preferable because it is 2.00 standard deviations below the mean and would correspond to the highest of the five different possible test scores.

C.

The z score of 2.00 is most preferable because it is 2.00 standard deviations above the mean and would correspond to the highest of the five different possible test scores.

D.

The z score of 1.00 is most preferable because it is 1.00 standard deviation below the mean and would correspond to an above average test score.

E.

The z score of 0 is most preferable because it corresponds to a test score equal to the mean.

#17

Researchers measured the data speeds for a particular smartphone carrier at 50 airports. The highest speed measured was 73.6 Mbps. The complete list of 50 data speeds has a mean of x=15.53 Mbps and a standard deviation of s=37.97 Mbps.

a. What is the difference betweencarrier's highest data speed and the mean of all 50 dataspeeds?

b. How many standard deviations is that[the difference found in part(a)]?

c. Convert thecarrier's highest data speed to a z score.

d. If we consider data speeds that convert to z scores between 2 and 2 to be neither significantly low nor significantlyhigh, is thecarrier's highest data speedsignificant?

a. The difference is _____Mbps.

(Type an integer or a decimal. Do notround.)

b. The difference is ______standard deviations.

(Round to two decimal places asneeded.)

c. The z score is z=______.

(Round to two decimal places asneeded.)

d. Thecarrier's highest data speed is ________(A- Significantly low, B- Significantly high, C-not significant)

#18

Use z scores to compare the given values.

The tallest living man at one time had a height of 233 cm. The shortest living man at that time had a height of 141.8 cm. Heights of men at that time had a mean of 174.01 cm and a standard deviation of 5.69 cm. Which of these two men had the height that was moreextreme?

Since the z score for the tallest man is z=______and the z score for the shortest man is z=_______, the ________(A-tallest, B- shortest) man had the height that was more extreme.

(Round to two decimalplaces.)

#19

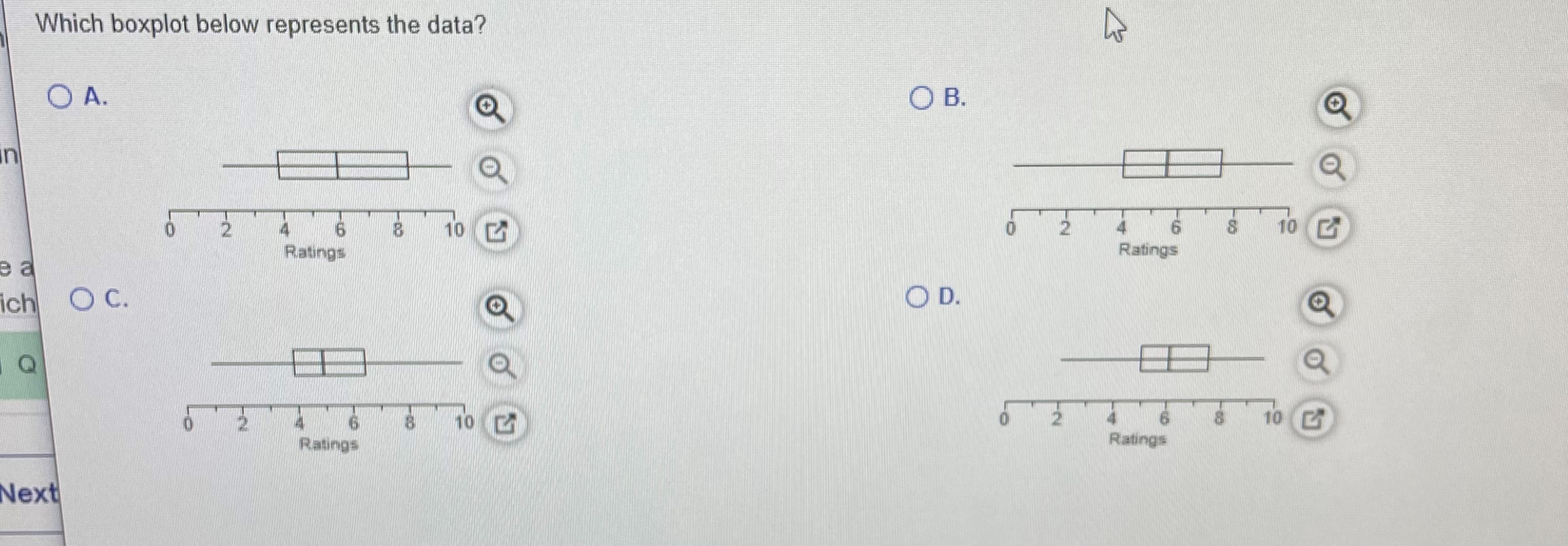
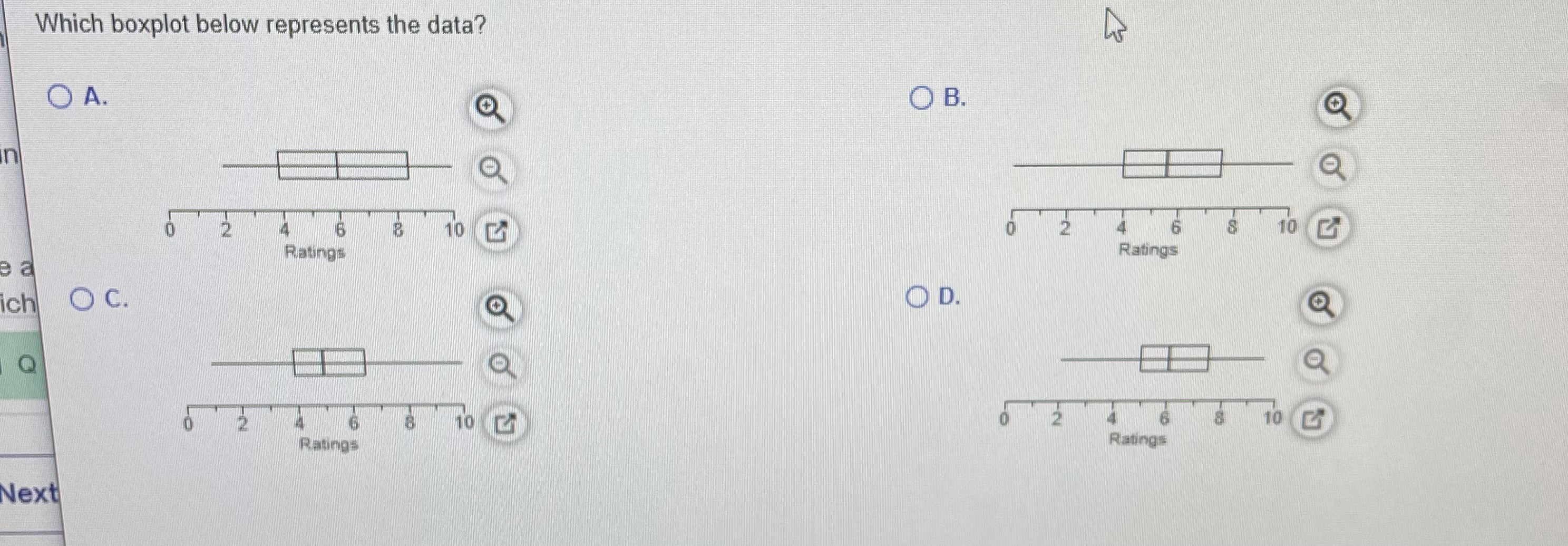
The following are the ratings of males by females in an experiment involving speed dating. Use the given data to construct a boxplot and identify the5-number summary.

2.0 3.0 3.5 4.0 5.0 5.0 6.0 6.0 6.0 6.0 6.0 7.0 7.0 7.5 7.5 7.5 8.0 9.0 9.5 9.5

The5-number summary is ______, _______, _______, _______, and .

(Use ascending order. Type integers or decimals. Do notround.)

Which boxplot below represents thedata?

Which boxplot below represents the data? O A. O B. In 0 2 4 6 10 2 6 10 Ratings Ratings ich O c. OD. Q 2 10 10 0 2 4 6 Ratings Ratings NextPulse rates for men and women -X Men's Pulse Rates Full data set 62 60 69 70 58 90 83 75 78 74 88 55 101 67 69 57 82 62 72 80 53 60 67 62 62 50 67 56 68 55 68 76 69 64 72 73 76 64 49 60 Women's Pulse Rates 77 66 67 72 78 78 100 70 63 80 70 58 78 77 77 89 95 62 99 99 74 63 84 64 71 79 75 90 90 71 83 73 80 106 61 73 71 90 76 80 WODetermine the boxplot for the men's pulse rate data. Choose the correct graph below O A OB. XX 40 50 60 70 80 90 100110 40 50 60 70 80 90 100110 O D. O ich 40 50 60 70 80 90 100110 40 50 60 70 80 90 100110Determine the boxplot for the women's boxplot data. Choose the correct graph below. OAT O B. X X in 40 50 80 70 80 90 100110 40 50 60 70 80 90 100110 O C. OD. ca X ich 40 50 60 70 30 90 100110 40 50 60 70 30 90 100110