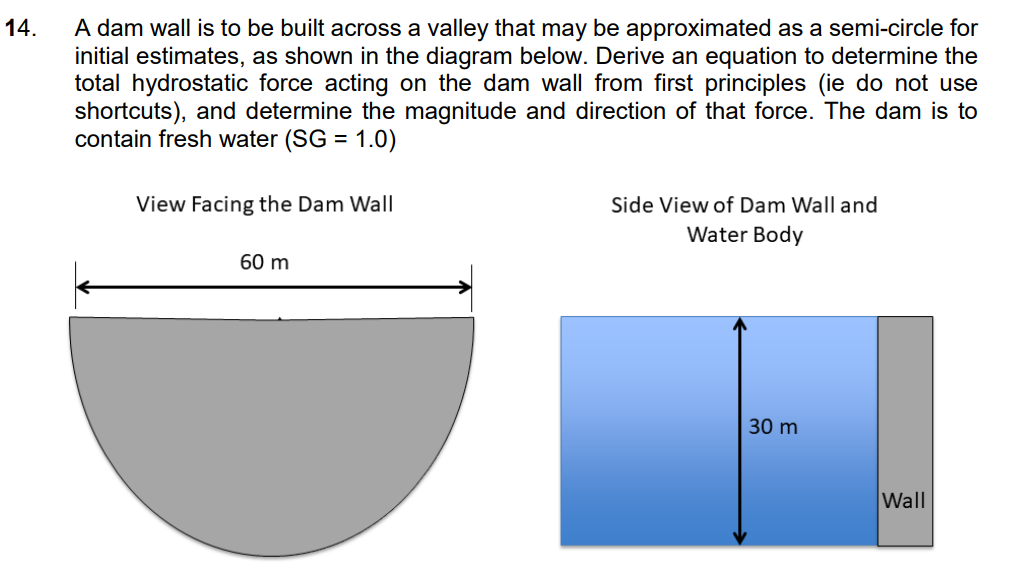
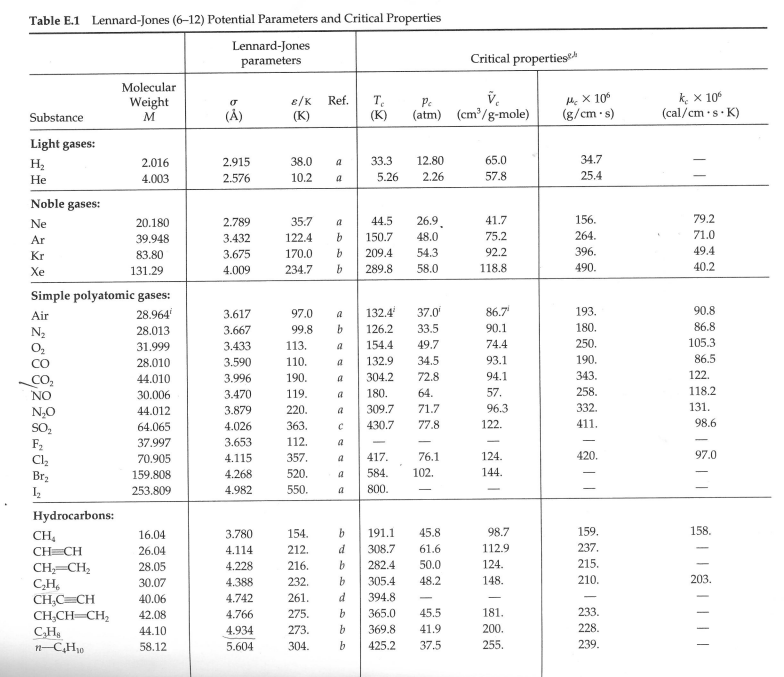
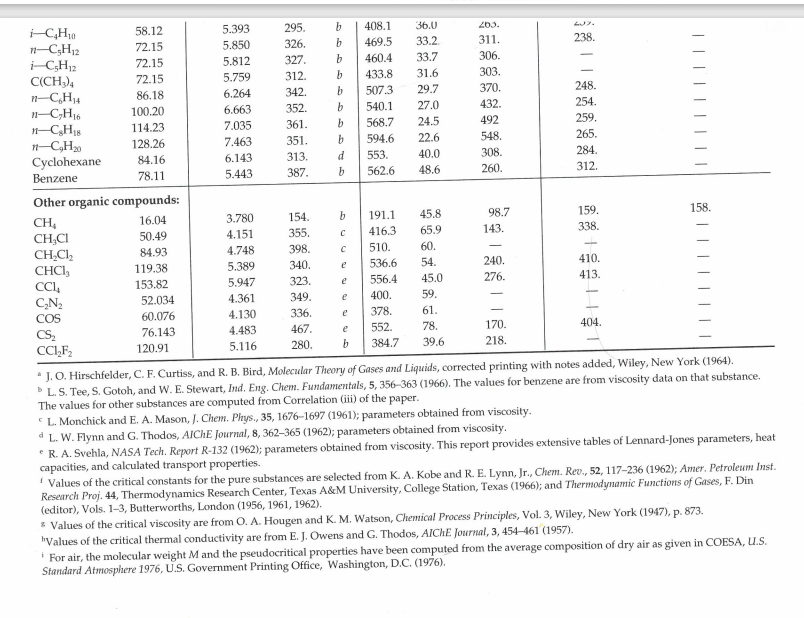
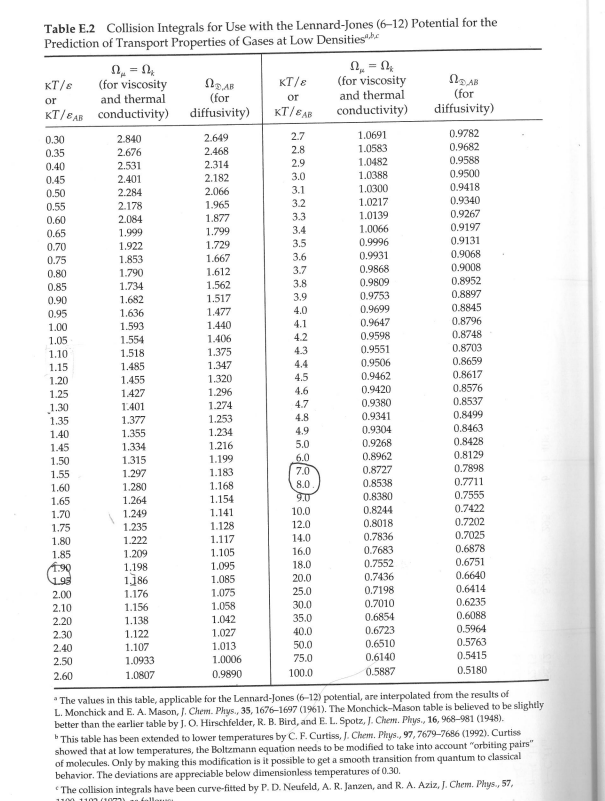
14. A dam wall is to be built across a valley that may be approximated as a semi-circle for initial estimates, as shown in the diagram below. Derive an equation to determine the total hydrostatic force acting on the dam wall from first principles (ie do not use shortcuts), and determine the magnitude and direction of that force. The dam is to contain fresh water (SG = 1.0) View Facing the Dam Wall 60 m Side View of Dam Wall and Water Body 30 m Wall Table E.1 Lennard-Jones (6-12) Potential Parameters and Critical Properties Lennard-Jones parameters Critical properties Molecular Weight Substance M () E/K Ref. T (K) (K) Pc (atm) (cm/g-mole) MX 106 (g/cms) k x 106 (cal/cm s.K) Light gases: H 2.016 2.915 38.0 a 33.3 12.80 65.0 34.7 He 4.003 2.576 10.2 a 5.26 2.26 57.8 25.4 Noble gases: Ne 20.180 2.789 35.7 a 44.5 26.9 41.7 156. 79.2 Ar 39.948 3.432 122.4 b 150.7 48.0 75.2 264. 71.0 Kr 83.80 3.675 170.0 b 209.4 54.3 92.2 396. 49.4 Xe 131.29 4.009 234.7 b 289.8 58.0 118.8 490. 40.2 Simple polyatomic gases: Air 28.964' 3.617 97.0 a 132.4' 37.0 86.7 193. 90.8 N 28.013 3.667 99.8 b 126.2 33.5 90.1 180. 86.8 31.999 3.433 113. a 154.4 49.7 74.4 250. 105.3 28.010 3.590 110. a 132.9 34.5 93.1 190. 86.5 44.010 3.996 190. a 304.2 72.8 94.1 343. 122. NO 30.006 3.470 119. a 180. 64. 557 57. 258. 118.2 NO 44.012 3.879 220. a 309.7 71.7 96.3 332. SO 64.065 4.026 363. 430.7 77.8 122. 411. 131. 98.6 F 37.997 3.653 112. a - - - Cl 70.905 4.115 357. a 417. 76.1 124. 420. 97.0 Br 159.808 4.268 520. a 584. 102. 144. I. 253.809 4.982 550. a 800. - Hydrocarbons: CH 16.04 3.780 154. b 191.1 45.8 98.7 159. CH=CH 26.04 4.114 212. d 308.7 61.6 112.9 237. CH2=CH2 28.05 4.228 216. b 282.4 50.0 124. 215. CH6 30.07 4.388 232. b 305.4 48.2 148. 210. CH,C=CH 40.06 4.742 261. d 394.8 - - CH,CH=CH2 42.08 4.766 275. b 365.0 45.5 181. 233. CHB 44.10 4.934 273. b 369.8 41.9 200. 228. n-CH10 58.12 5.604 304. b 425.2 37.5 255. 239. | | | | | | 158. 203. i-C4H10 58.12 5.393 295. b 408.1 36.0 203. 633. n-C5H12 72.15 5.850 326. b 469.5 33.2 311. 238. i-C5H12 72.15 5.812 327. b 460.4 33.7 306. C(CH3)4 72.15 5.759 312. b 433.8 31.6 303. n-C6H14 86.18 6.264 342. b 507.3 29.7 370. 248. n-C,H16 100.20 6.663 352. b 540.1 27.0 432. 254. 11-C8H18 114.23 7.035 361. b 568.7 24.5 492 259. n-C,H20 128.26 7.463 351. b 594.6 22.6 548. 265. Cyclohexane 84.16 6.143 313. d 553. 40.0 308. 284. Benzene 78.11 5.443 387. b 562.6 48.6 260. 312. Other organic compounds: CH 16.04 3.780 154. b 191.1 45.8 98.7 159. 158. CHCl 50.49 4.151 355. 416.3 65.9 143. 338. CHCh 84.93 4.748 398. 510. 60. - CHCl3 119.38 5.389 340. e 536.6 54. 240. 410. CC14 153.82 5.947 323. e 556.4 45.0 276. 413. CN 52.034 4.361 349. e 400. 59. 60.076 4.130 336. e 378. 61. CS 76.143 4.483 467. e 552. 78. 170. 404. CCF 120.91 5.116 280. b 384.7 39.6 218. *J. O. Hirschfelder, C. F. Curtiss, and R. B. Bird, Molecular Theory of Gases and Liquids, corrected printing with notes added, Wiley, New York (1964). L. S. Tee, S. Gotoh, and W. E. Stewart, Ind. Eng. Chem. Fundamentals, 5, 356-363 (1966). The values for benzene are from viscosity data on that substance. The values for other substances are computed from Correlation (iii) of the paper. L. Monchick and E. A. Mason, J. Chem. Phys., 35, 1676-1697 (1961); parameters obtained from viscosity. d L. W. Flynn and G. Thodos, AIChE Journal, 8, 362-365 (1962); parameters obtained from viscosity. R. A. Svehla, NASA Tech. Report R-132 (1962); parameters obtained from viscosity. This report provides extensive tables of Lennard-Jones parameters, heat capacities, and calculated transport properties. Values of the critical constants for the pure substances are selected from K. A. Kobe and R. E. Lynn, Jr., Chem. Rev., 52, 117-236 (1962); Amer. Petroleum Inst. Research Proj. 44, Thermodynamics Research Center, Texas A&M University, College Station, Texas (1966); and Thermodynamic Functions of Gases, F. Din (editor), Vols. 1-3, Butterworths, London (1956, 1961, 1962). Values of the critical viscosity are from O. A. Hougen and K. M. Watson, Chemical Process Principles, Vol. 3, Wiley, New York (1947), p. 873. "Values of the critical thermal conductivity are from E. J. Owens and G. Thodos, AIChE Journal, 3, 454-461 (1957). For air, the molecular weight M and the pseudocritical properties have been computed from the average composition of dry air as given in COESA, U.S. Standard Atmosphere 1976, U.S. Government Printing Office, Washington, D.C. (1976). DAB or and thermal (for KT/EAB conductivity) diffusivity) Table E.2 Collision Integrals for Use with the Lennard-Jones (6-12) Potential for the Prediction of Transport Properties of Gases at Low Densities" KT/8 (for viscosity and thermal conductivity) (for diffusivity) = KT/e (for viscosity or KT/BAB 0.30 2.840 2.649 2.7 1.0691 0.9782 0.35 2.676 2.468 2.8 1.0583 0.9682 0.40 2.531 2.314 2.9 1.0482 0.9588 0.45 2.401 2.182 3.0 1.0388 0.9500 0.50 2.284 2.066 3.1 1.0300 0.9418 0.55 2.178 1.965 3.2 1.0217 0.9340 0.60 2.084 1.877 3.3 1.0139 0.9267 0.65 1.999 1.799 3.4 1.0066 0.9197 0.70 1.922 1.729 3.5 0.9996 0.9131 0.75 1.853 1.667 3.6 0.9931 0.9068 0.80 1.790 1.612 3.7 0.9868 0.9008 0.85 1.734 1.562 3.8 0.9809 0.8952 0.90 1.682 1.517 3.9 0.9753 0.8897 0.95 1.636 1.477 4.0 0.9699 0.8845 1.00 1.593 1.440 4.1 0.9647 0.8796 1.05 1.554 1.406 4.2 0.9598 0.8748 1.10 1.518 1.375 4.3 0.9551 0.8703 1.15 1.485 1.347 4.4 0.9506 0.8659 1.20 1.455 1.320 4.5 0.9462 0.8617 1.25 1.427 1.296 4.6 0.9420 0.8576 1.30 1.401 1.274 4.7 0.9380 0.8537 1.35 1.377 1.253 4.8 0.9341 0.8499 1.40 1.355 1.234 4.9 0.9304 0.8463 1.45 1.334 1.216 5.0 0.9268 0.8428 1.50 1.315 1.199 6.0 0.8962 0.8129 1.55 1.297 1.183 7.0 0.8727 0.7898 1.60 1.280 1.168 8.0 0.8538 0.7711 1.65 1.264 1.154 9.0 0.8380 0.7555 1.70 1.249 1.141 10.0 0.8244 0.7422 1.75 1.235 1.128 12.0 0.8018 0.7202 1.80 1.222 1.117 14.0 0.7836 0.7025 1.85 1.209 1.105 16.0 0.7683 0.6878 1.90 1.198 1.095 18.0 0.7552 0.6751 198 1,186 1.085 20.0 0.7436 0.6640 2.00 1.176 1.075 25.0 0.7198 0.6414 2.10 1.156 1.058 30.0 0.7010 0.6235 2.20 1.138 1.042 35.0 0.6854 0.6088 2.30 1.122 1.027 40.0 0.6723 0.5964 2.40 1.107 1.013 50.0 0.6510 0.5763 2.50 1.0933 1.0006 75.0 0.6140 0.5415 2.60 1.0807 0.9890 100.0 0.5887 0.5180 "The values in this table, applicable for the Lennard-Jones (6-12) potential, are interpolated from the results of L. Monchick and E. A. Mason, J. Chem. Phys., 35, 1676-1697 (1961). The Monchick-Mason table is believed to be slightly better than the earlier table by J. O. Hirschfelder, R. B. Bird, and E. L. Spotz, J. Chem. Phys., 16, 968-981 (1948). This table has been extended to lower temperatures by C. F. Curtiss, J. Chem. Phys., 97, 7679-7686 (1992). Curtiss showed that at low temperatures, the Boltzmann equation needs to be modified to take into account "orbiting pairs" of molecules. Only by making this modification is it possible to get a smooth transition from quantum to classical behavior. The deviations are appreciable below dimensionless temperatures of 0.30. "The collision integrals have been curve-fitted by P. D. Neufeld, A. R. Janzen, and R. A. Aziz, J. Chem. Phys., 57, 1100 1100 (1977)