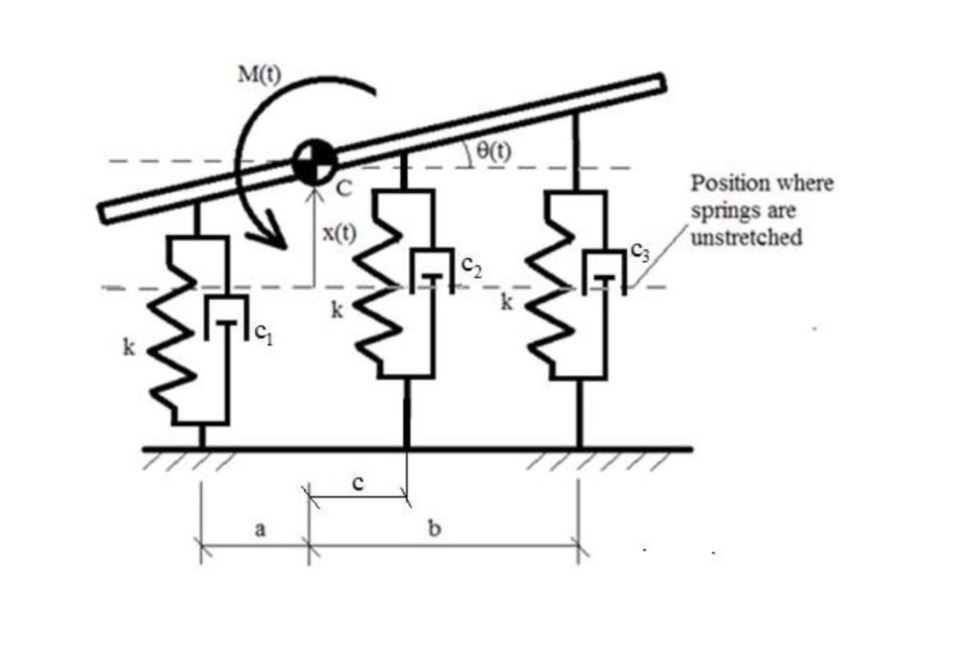
2. Consider a slab with mass m and moment of inertia I about its center of mass C, supported by three vertical springs in parallel to viscous dampers, and forced by the moment applied about its center of mass. The system is at equilibrium when x = 0 = 0. Do not take into account gravity. See diagram below. a. Find the equations of motion, and define the mass, stiffness and damping matrices. Assume there is some non-zero applied moment M(t). For the undamped, unforced system: b. Compute the natural frequencies and mode shapes for m = 1 [kg], I = 5 [kg m], k = 500 [N/m], a = c = 0.8 [m], b = 1.2 [m]. Show that the mode shapes are orthogonal with respect to the mass or stiffness matrix. C. d. e. Use modal analysis/modal coordinates to compute the response of the undamped, unforced system for the following initial conditions: x(0) = 0 [m], x(0) = 0.2 [m/s], 0(0) = 20 [rad], (0) = 0 [rad/s]. Orthonormalize the modes found in (b). Show that this decouples the equations of motion. 1 Now assume there is some non-zero damping in the system: f. How should C, C2, and c3 be defined such that the system is proportionally damped? g. Show that the orthonormalized modes you calculated in (d) also decouple this damping matrix. h. Finally, assuming the values above and the damping matrix is given by C = BK, with B = 0.05, find the steady state response of the system x(t) and 8(t) to the external forcing M(t) = 2cos(3t). k M(t) a k b e(t) C3 Position where springs are unstretched