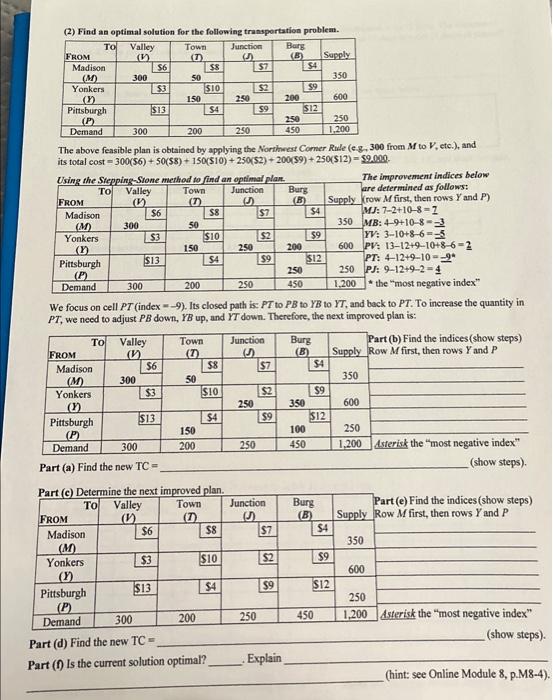
(2) Find an optimal solution for the following transportation problem. To Town (1) FROM Madison (M) Yonkers (Y) Pittsburgh (P) Demand FROM Madison (M) Yonkers (Y) Pittsburgh (P) Demand FROM Madison (M) Yonkers (Y) Valley (1) 300 FROM To Valley (1) To Madison (M) Yonkers (Y) Pittsburgh (P) Demand 300 300 Using the Stepping-Stone method to find an optimal plan. Town Junction (7) (1) Valley (1) 300 $13 $6 $3 $13 $6 $3 300 200 250 The above feasible plan is obtained by applying the Northwest Corner Rule (e.g., 300 from M to V, etc.), and its total cost = 300($6) +50($8) + 150($10) +250($2) +200($9) + 250($12) = $9,000. Pittsburgh (P) Demand 300 Part (a) Find the new TC = $6 $3 $13 $6 $3 $13 50 150 50 150 Town (7) 50 150 200 $8 $10 Town (7) $4 200 Part (c) Determine the next improved plan. To Valley (1) $8 $10 300 Part (d) Find the new TC = Part (f) Is the current solution optimal? $4 $8 $10 $4 Junction (J) $8 $10 250 $4 200 We focus on cell PT (index = -9). Its closed path is: PT to PB to YB to YT, and back to PT. To increase the quantity in PT, we need to adjust PB down, YB up, and YT down. Therefore, the next improved plan is: 250 250 $7 $2 250 $9 250 250 $7 $2 Junction () $9 $7 $2 $9 Junction () $7 $2 Burg (B) Supply $4 200 $9 Explain 250 450 200 $12 Burg (B) 250 450 $9 350 $4 100 450 $9 $12 Burg (B) $4 $9 $12 450 Burg (B) 250 1,200 350 600 The improvement indices below are determined as follows: Supply (row M first, then rows Y and P) MJ: 7-2+10-8=1 $4 $9 $12 350 600 250 1,200 MB: 4-9+10-8=-3 YV: 3-10+8-6=-5 PV: 13-12+9-10+8-6=2 350 Part (b) Find the indices (show steps) Supply Row M first, then rows Y and P 600 PT: 4-12+9-10=-9* PJ: 9-12+9-2=4 *the "most negative index" 250 1,200 Asterisk the "most negative index" (show steps). Part (e) Find the indices (show steps) Supply Row M first, then rows Y and P 350 600 250 1,200 Asterisk the "most negative index" (show steps). (hint: see Online Module 8, p.M8-4).

(2) Find an optimal soletion for the following transportation problem. The above feasible plan is obtained by applying the Northnest Comer Rule (ez, 300 from M to V, ete.), and its total cost =300(56)+50($8)+150($10)+250($2)+200($9)+250($12)=$9.000. The improvement indices below are determined as follows: (row M first, then rows Y and P ) MJ:72+108=7MB:49+108=3YV:310+86=5PV:1312+910+86=2PT:412+910=9PJ:912+92=4*the"mostnegativeindex" We focus on cell PT (index =9 ). Its closed path is: PT to PB to YB to YT, and back to PT. To increase the quantity in PT, we need to adjust PB down, YB up, and YT down. Therefore, the next improved plan is: Part (d) Find the new TC = (show steps). Part (f) Is the current solution optimal? Explain (hint: see Online Module 8, p.M8-4)