2.

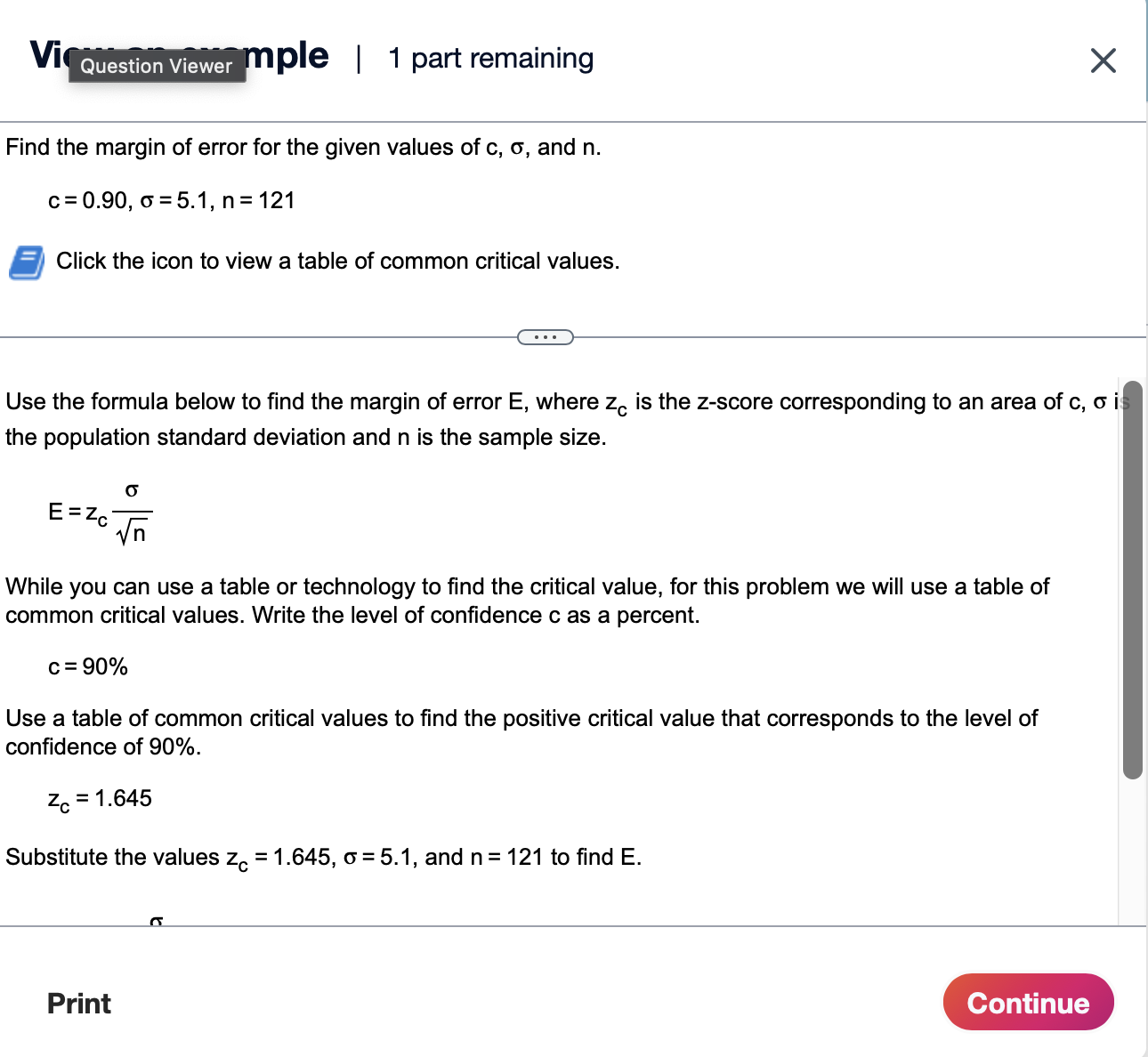
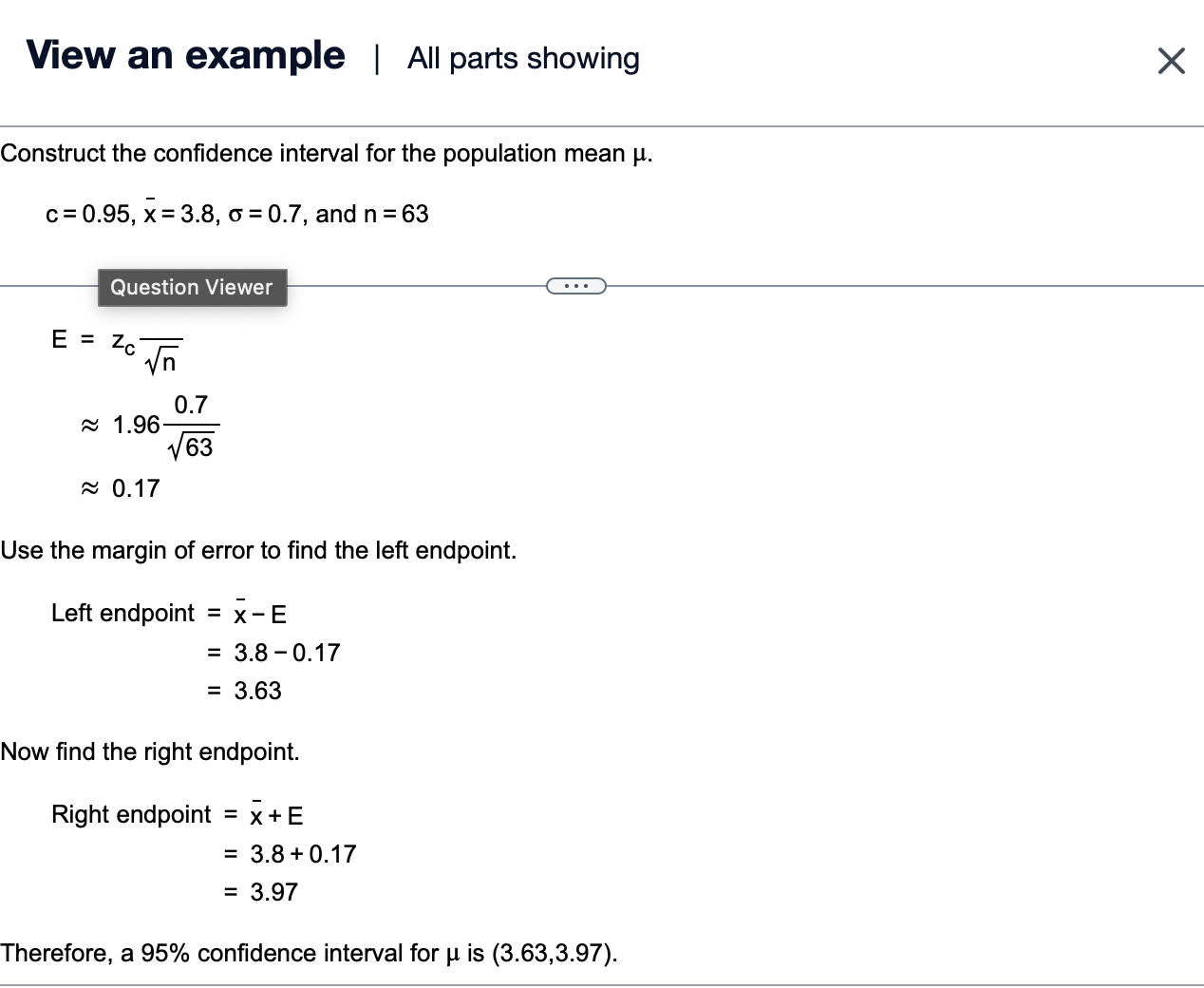
Find the margin of error for the given values of c, o, and n. c=0.95,6=2.6,n=100 5' Click the icon to view a table of common critical values. Question Viewer E= |:| (Round to three decimal places as needed.) Vigaeosypwample | 1 part remaining X Find the margin of error for the given values of , 6, and n. c=0.90,0=5.1,n=121 g Click the icon to view a table of common critical values. Use the formula below to find the margin of error E, where z, is the z-score corresponding to an area of , i the population standard deviation and n is the sample size. o E=Zc While you can use a table or technology to find the critical value, for this problem we will use a table of common critical values. Write the level of confidence as a percent. c=90% Use a table of common critical values to find the positive critical value that corresponds to the level of confidence of 90%. 2, =1.645 Substitute the values z, =1.645, 6 =5.1, and n =121 to find E. While you can use a table or technology to find the critical value, for this problem we will use a table of common critical values. Write the level of confidence c as a percent. c=90% Use a table of common critical values to find the positive critical value that corresponds to the level of confidence of 90%. z,=1.645 Substitute the values z, =1.645, 6=5.1, and n=121 to find E. o Z_ C Jn : A ~ 1.645 Y121 0.763 Q Find the margin of error for the given values of , o, and n. c=0.95,6=3.9,n=100 g Click the icon to view a table of common critical values. E= D (Round to three decimal places as needed.) View an example | All parts showing X Find the margin of error for the given values of , 5, and n. c=0.90,6=5.1,n=121 @ Click the icon to view a table of common critical values. () Use the formula below to find the margin of error E, where z, is the z-score corresponding to an area of , is the population standard deviation and n is the sample size. o E=Zc While you can use a table or technology to find the critical value, for this problem we will use a table of common critical values. Write the level of confidence as a percent. c=90% Use a table of common critical values to find the positive critical value that corresponds to the level of confidence of 90%. z,=1.645 Substitute the values z, =1.645, 6=5.1, and n=121 to find E. e eeeem e me e s e it e mram ot s m s m e e e = e n o e c=90% Use a table of common critical values to find the positive critical value that corresponds to the level of confidence of 90%. z,=1.645 Substitute the values z, =1.645, 6=5.1, and n=121 to find E. O Z C 1/5 5.1 ~ 1.645 4121 0.763 R Therefore, the margin of error is approximately 0.763. Construct the confidence interval for the population mean p. c=0.90, x=9.5, 6=0.3, and n=57 - e 5 A 90% confidence interval for p is (D,[D . (Round to two decimal places as needed.) View an example | All parts showing X Construct the confidence interval for the population mean p. c=0.95 x=3.8,6=0.7, and n =63 = Find the left and right endpoints and form the confidence interval for the population mean p as shown below. Use the formula E=z, to find the margin of error, where z,, is the z-score corresponding to an area of c, c Jn o is the population standard deviation and n is the sample size. Left endpoint: x-E Right endpoint: X+E The level of confidence c is the area under the standard normal curve between the critical values -z and z.. 1 The area outside the critical values is 1 - , so the area in each tail is E('I -C). Substitute the value of and evaluate to find the area in each tail. 11 11095 5( c) 5( .95) 0.025 While you can use a standard normal table or technology to find the critical value, for this problem we will use a standard normal table. View an example | All parts showing Construct the confidence interval for the population mean p. c=0.95,x=38,6=0.7, and n=63 D Use a standard normal table to find the positive critical value that corresponds to a tail area of 0.025. z,=1.96 Substitute the values z, =1.96, 6=0.7, and n=63 to find E. o - Z. c\\/ 0.7 ~ 1.96 Y63 ~ 0.17 Use the margin of error to find the left endpoint. x-E 3.8-0.17 3.63 Left endpoint A ... % L . L N L View an example | All parts showing X Construct the confidence interval for the population mean p. c=0.95 x=3.8,6=0.7, and n=63 E=2z. yn - 58 0.7 463 ~ 017 Use the margin of error to find the left endpoint. Left endpoint = x-E = 3.8-0.17 = 3.63 Now find the right endpoint. Right endpoint = x+E 3.8+0.17 3.97 Therefore, a 95% confidence interval for p is (3.63,3.97)