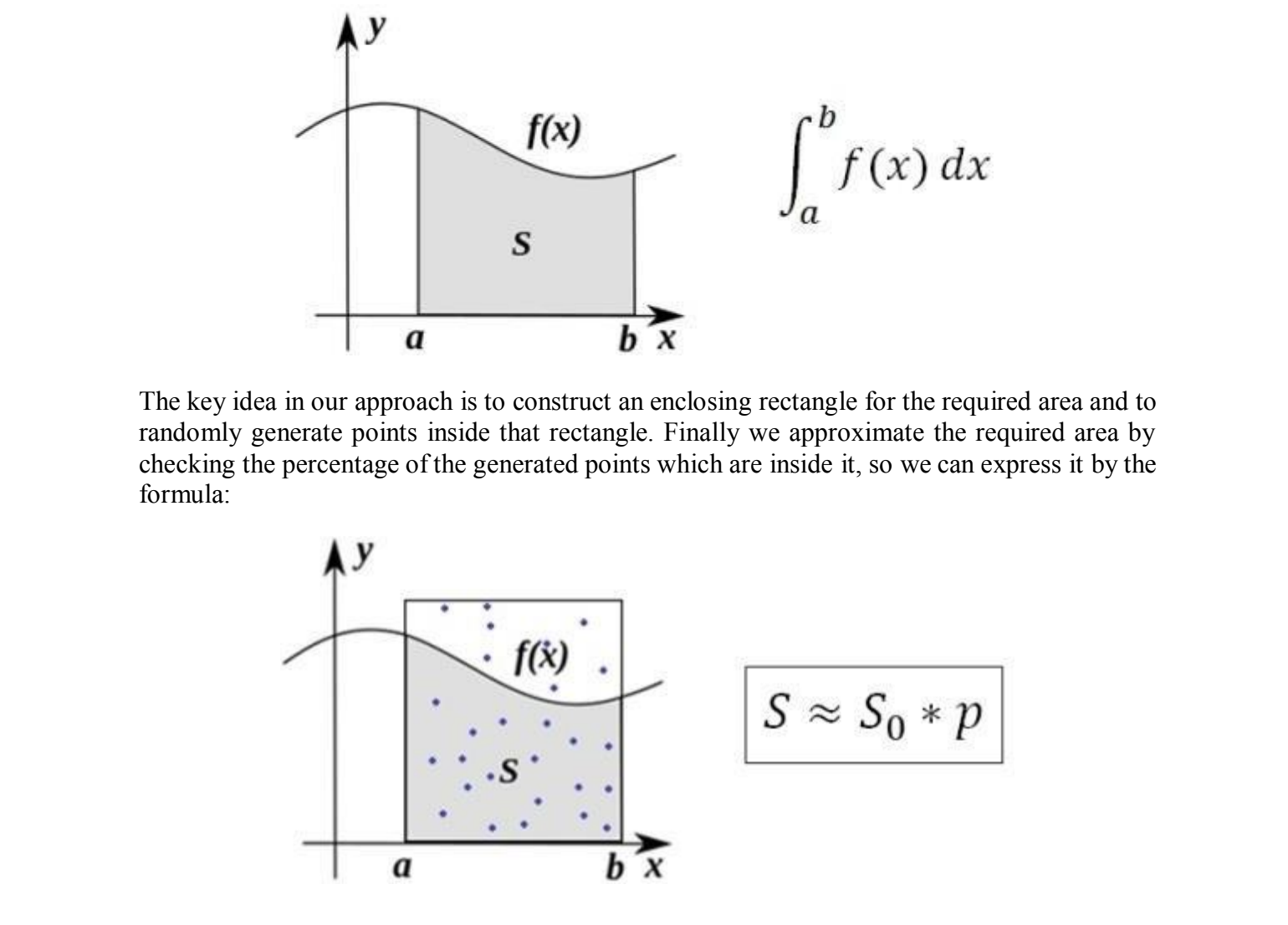
$2$

Here S is denoting the required area $($under the curve$)$ depicted in grey in the above figures, S$0$

is the area of the enclosing rectangle and p is a value between $0$ and $1$ representing the ratio of

the generated points which fall inside the S area $($grey zone in the figure$)$ divided by the total

number of points. For example in the figure above we would have p $=19/270\mathrm{.}7037$

The function whose definite integral will be calculated, will be given in hardcoded way in the

form of a function $($but notice that our basic method works only for the cases when the values

of the function in the integration interval are always non$-$negative$)$:

In this problem you are required to write a parallel program which will estimate the value of a

definite integral. The program will create several parallel units and each of them will generate

random points inside the enclosing rectangle. Finally the definite integral will be estimated as:

N$0$

Definite integral $$

N

Area of enclosing rectagle

Here, N is the total number of generated random points by all threads and N$0$ is the number of

random points which are located below the curve.

a$.$ Write a programusing POSIX threads which receives as command line parameters the total

number of random points $($N$)$ that will be generated, the number ofthreads that will be used,

the bounds of the definite integral, an upper bound on the values of the function in this

interval, and will estimate the value of the definite integral using the Monte Carlo method

described above. A sample execution may be:

$./$MonteCarloIntegralEstimator $20000001001\mathrm{.}52\mathrm{.}5$

b$.$ Write a program using OpenMP which receives as command line parameters the total

number of random points $($N$)$ that will be generated, the number of threads that will be used,

the bounds of the definite integral, an upper bound on the values of the function in this

interval, and will estimate the value of the definite integral using the Monte Carlo method

described above. A sample execution may be:

$./$MonteCarloIntegralEstimator $20000001001\mathrm{.}52\mathrm{.}5$

c$.$ Write a program using MPI which reads as input from the user $($only once$)$ the total number

of random points $($N$)$ that will be generated, the bounds of the definite integral, an upper

bound on the values ofthe function in this interval, and will estimate the value ofthe definite

integral using the Monte Carlo method described above. The number of processes will be

provided to the mpiexec command. A sample execution may be:

mpiexec $-$n $10./$MonteCarloIntegralEstimator

An example that may be used for testing purposes:

f$($x$)=$ x$2,$ from $1$ to $3,$ as an upper bound may use $10($any value greater than $9$ is fine$),$ and

the expected result is $8\mathrm{.}66666.($In this case the enclosing rectangle is determined by the lines

x $=1,$ x $=3,$ y $=0,$ y $=10,$ so its area is $20.$ If we generate $100000$ points and $43345$ points

are below the curve, then the approximation of the integral for this case is:

$43345$

Definite integral $$

$10000020=8\mathrm{.}669{\displaystyle \underset{a}{\overset{b}{}}}f(x)dx$

The key idea in our approach is to construct an enclosing rectangle for the required area and to

randomly generate points inside that rectangle. Finally we approximate the required area by

checking the percentage of the generated points which are inside it$,$ so we can express it by the

formula: