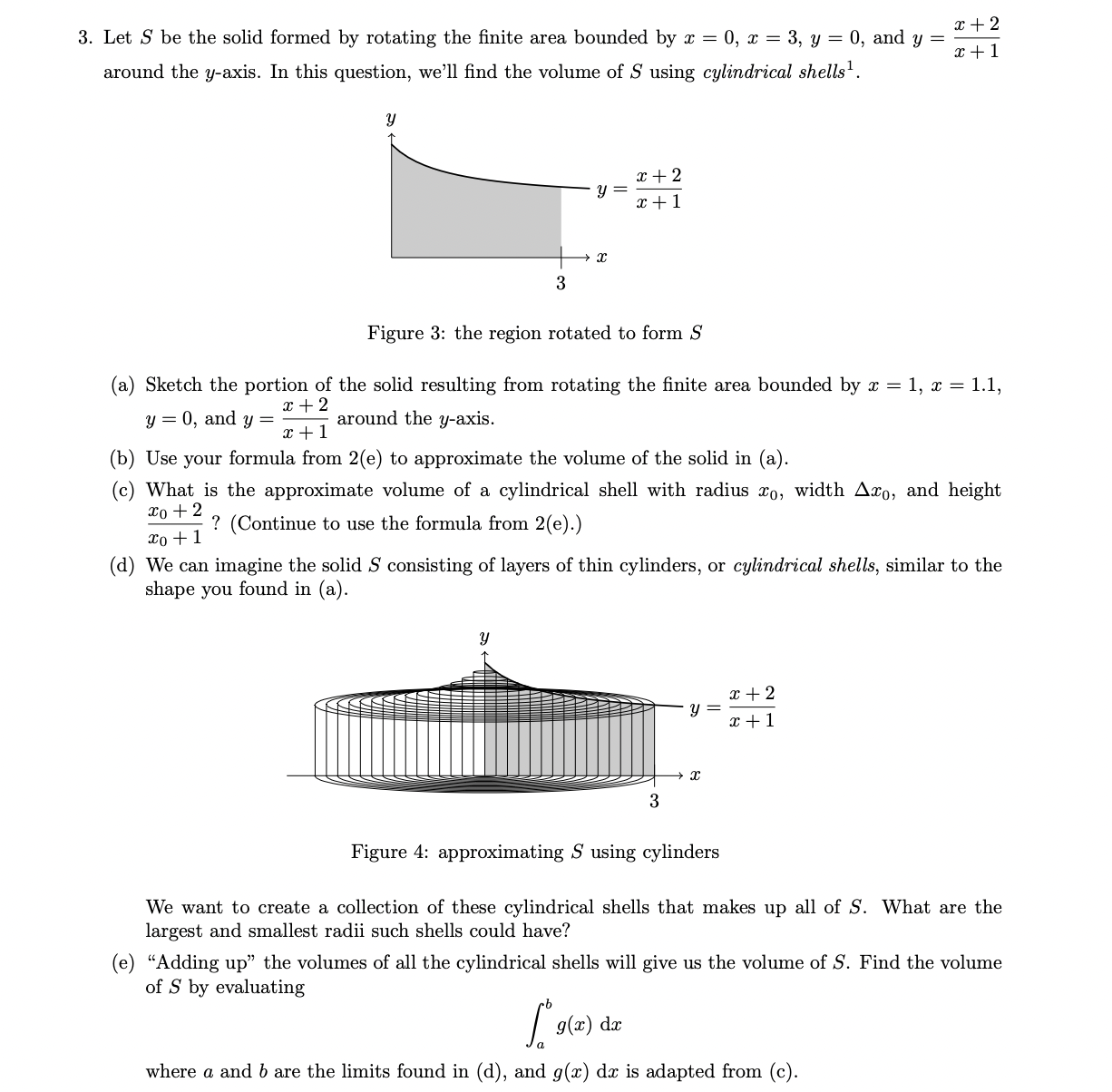
2. In this question, we'll approximate the volume of a thin cylinder. The approximation may seem odd at first, but it will be useful later on. (x + Ax) = x 2 (a) Let x be a positive constant. Evaluate lim Ax0 (b) Let R be a washer-shaped region with inner radius x and outer radius x + A. Give the area of R. X x + Ax Figure 1: region R (c) Let Ax be a positive number, close to 0. Give a geometric argument for why the area of R might be close to 2xAx. (Hint: imagine unrolling" the circle.) (d) Use part (a) to further justify why the area of R might be close to 27xAx when Ax is a positive number that is close to 0. (e) Imagine a thin cylinder whose base is R and height is y. Use the approximate area from (c) to give an approximate volume of the cylinder. Figure 2: thin cylinder 3. Let S be the solid formed by rotating the finite area bounded by x = 0, x = 3, y = 0, and y around the y-axis. In this question, we'll find the volume of S using cylindrical shells. Y y = 0, and y = 3 y = X Figure 3: the region rotated to form S (a) Sketch the portion of the solid resulting from rotating the finite area bounded by x = 1, x = 1.1, x + 2 around the y-axis. Y x + 2 x + 1 x + 1 (b) Use your formula from 2(e) to approximate the volume of the solid in (a). (c) What is the approximate volume of a cylindrical shell with radius o, width Axo, and height xo + 2 ? (Continue to use the formula from 2(e).) xo +1 (d) We can imagine the solid S consisting of layers of thin cylinders, or cylindrical shells, similar to the shape you found in (a). 3 x + 2 x+1 x + 2 y = x+1 g(x) dx X Figure 4: approximating S using cylinders We want to create a collection of these cylindrical shells that makes up all of S. What are the largest and smallest radii such shells could have? (e) "Adding up" the volumes of all the cylindrical shells will give us the volume of S. Find the volume of 5 by evaluating S where a and b are the limits found in (d), and g(x) dx is adapted from (c).