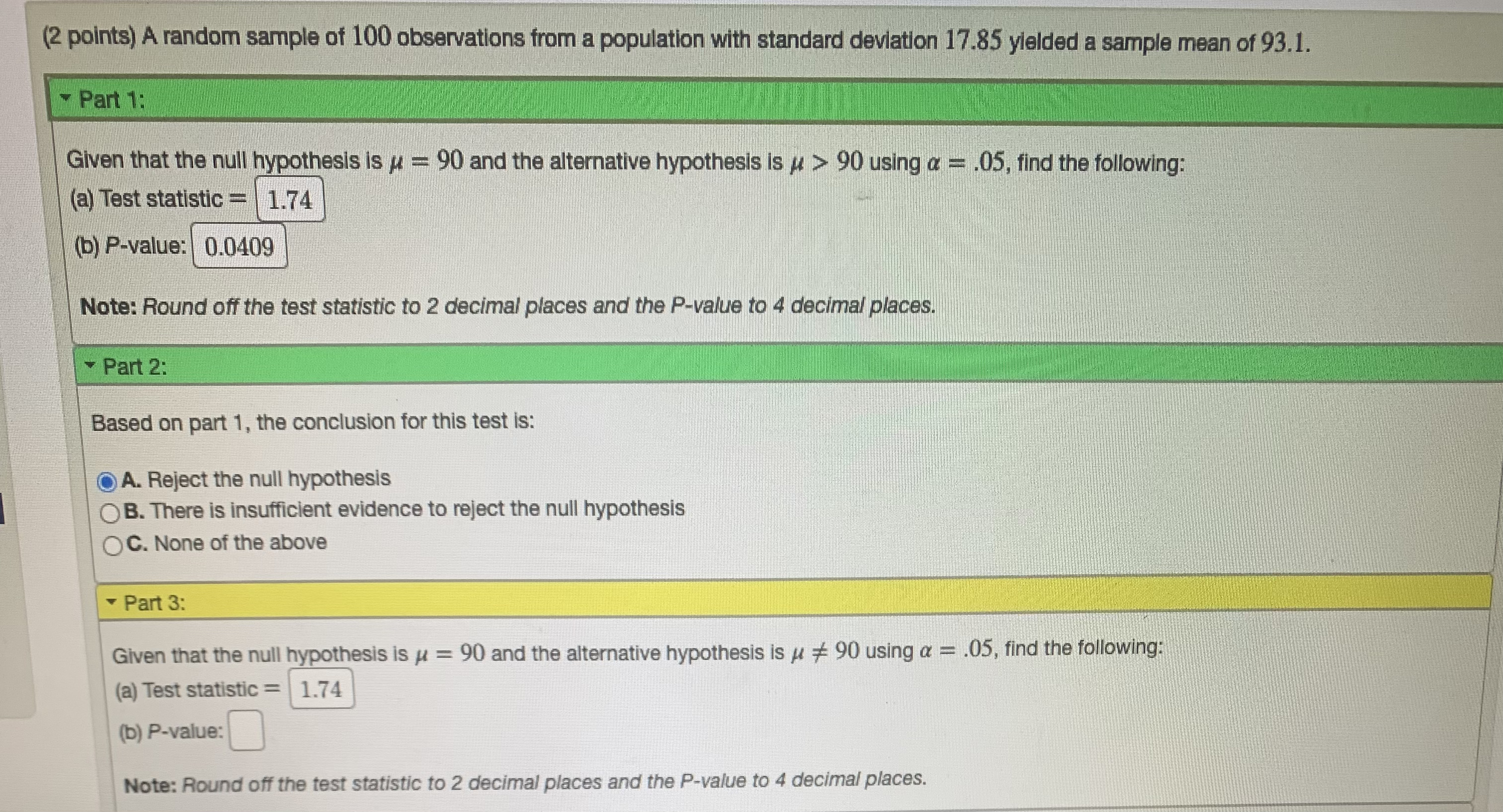
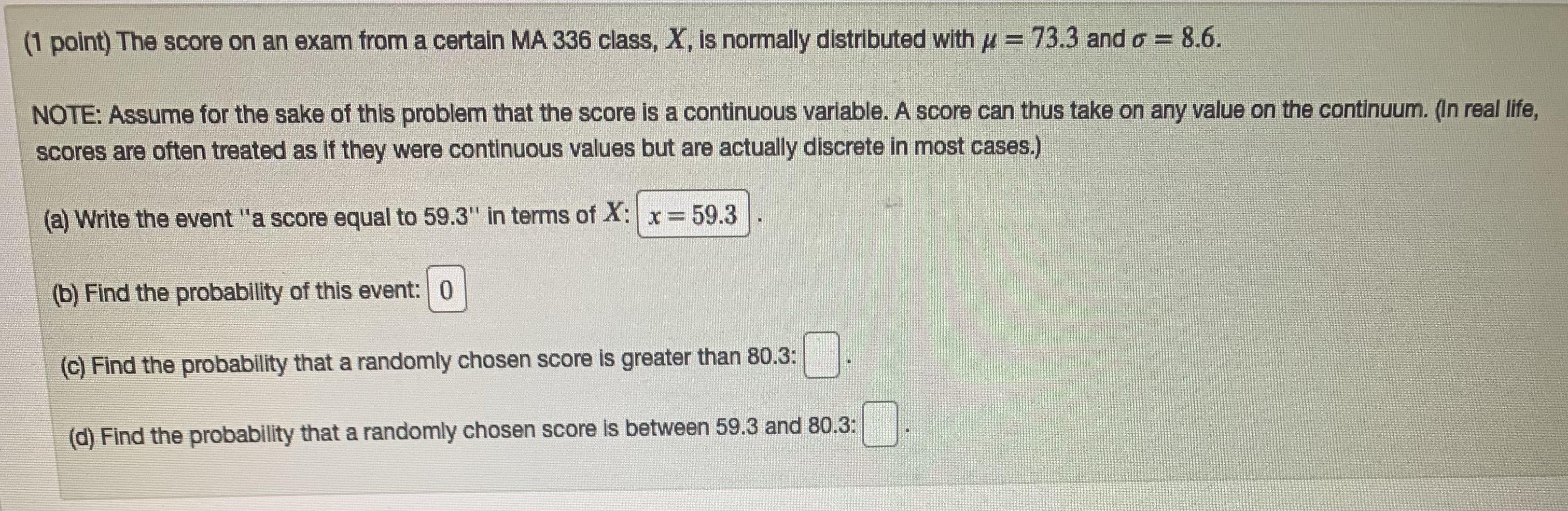
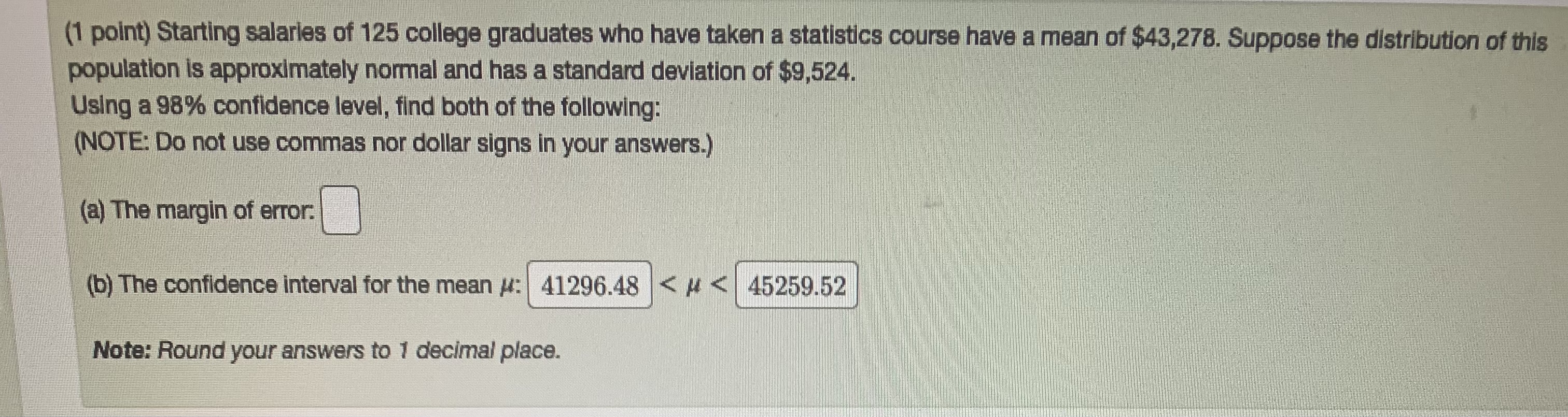
(2 points) A random sample of 100 observations from a population with standard deviation 17.85 yielded a sample mean of 93.1. Part 1: Given that the null hypothesis is / = 90 and the alternative hypothesis is # > 90 using a = .05, find the following: (a) Test statistic = 1.74 (b) P-value: | 0.0409 Note: Round off the test statistic to 2 decimal places and the P-value to 4 decimal places. Part 2: Based on part 1, the conclusion for this test is: O A. Reject the null hypothesis OB. There is insufficient evidence to reject the null hypothesis O C. None of the above Part 3: Given that the null hypothesis is / = 90 and the alternative hypothesis is # # 90 using a = .05, find the following: (a) Test statistic = 1.74 (b) P-value: Note: Round off the test statistic to 2 decimal places and the P-value to 4 decimal places.(3 points) Consider a population of 5 literature students. Each student was assigned a final paper assignment. For each student (S, for student 1, $2 for student 2, etc.), the number of pages the student wrote for his or her paper is listed below: S1 = 81, $2 = 19, $3 = 43, S4 = 15, $5 = 38 This is a multi-step problem. Part 1: Find the mean of the population. Round to 4 decimal places if necessary. Answer. 39.2 Part 2: Find the standard deviation of the population. Round to 4 decimal places if necessary. Answer.(1 point) The score on an exam from a certain MA 336 class, X, is normally distributed with # = 73.3 and o = 8.6. NOTE: Assume for the sake of this problem that the score is a continuous variable. A score can thus take on any value on the continuum. (In real life, scores are often treated as if they were continuous values but are actually discrete in most cases.) (a) Write the event "a score equal to 59.3" in terms of X: x = 59.3 (b) Find the probability of this event: 0 (c) Find the probability that a randomly chosen score is greater than 80.3: (d) Find the probability that a randomly chosen score is between 59.3 and 80.3:(1 point) Starting salaries of 125 college graduates who have taken a statistics course have a mean of $43,278. Suppose the distribution of this population is approximately normal and has a standard deviation of $9,524. Using a 98% confidence level, find both of the following: (NOTE: Do not use commas nor dollar signs in your answers.) (a) The margin of error (b) The confidence interval for the mean /: 41296.48 45259.52 Note: Round your answers to 1 decimal place