Question
2. Problem C-5.16 from textbook. You can use the following algorithm for this purpose (assuming that the pegs (i.e. rods) are labeled as a, b,
2. Problem C-5.16 from textbook. You can use the following algorithm for this purpose (assuming that the pegs (i.e. rods) are labeled as a, b, and c, and the disks are on peg a and we want to move the disks from peg a to peg c using peg b as temporary storage). void Tower_of_Hanoi(int n, char from_peg, char to_peg, char temp_peg) if (n == 0) return; //base case Move n-1 disks from from_peg to temp_peg using to_peg as helper (i.e. temporary storage) by making a recursive call Move the last disk (nth disk) from from_peg to to_peg (implement this move as a print statement that moves the last disk to to_peg) Move n-1 disks from temp_peg to to_peg using from_peg as helper (i.e. temporary storage) by making a recursive call. Implement this algorithm using recursion and write a main method to test your method.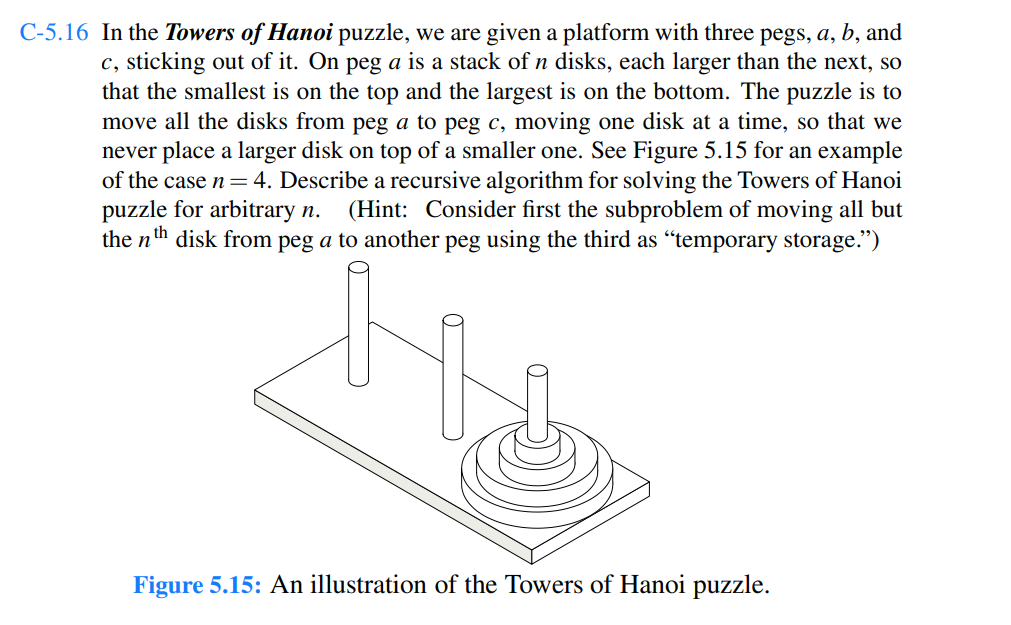
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


