Answered step by step
Verified Expert Solution
Question
1 Approved Answer
2. Prove that if f: D R is continuous at xo E D, then f|: D - R, defined by |f|(x) = |f(x)|, is
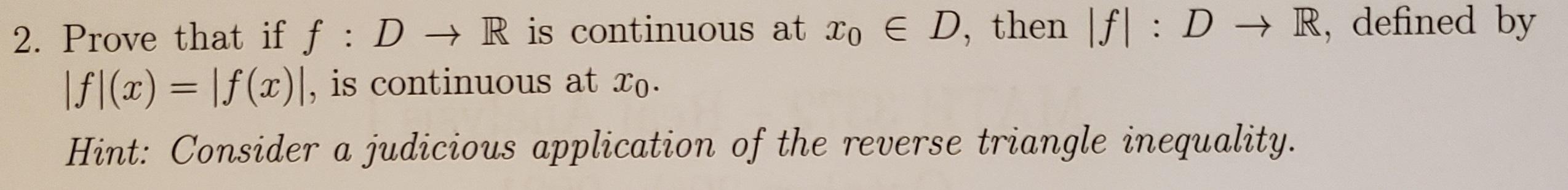
2. Prove that if f: D R is continuous at xo E D, then f|: D - R, defined by |f|(x) = |f(x)|, is continuous at xo. Hint: Consider a judicious application of the reverse triangle inequality.
Step by Step Solution
★★★★★
3.51 Rating (158 Votes )
There are 3 Steps involved in it
Step: 1
2 aiven fD IR is Con tinuoug at 2 ED tohe...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
An Introduction to the Mathematics of financial Derivatives
Authors: Salih N. Neftci
2nd Edition
978-0125153928, 9780080478647, 125153929, 978-0123846822
