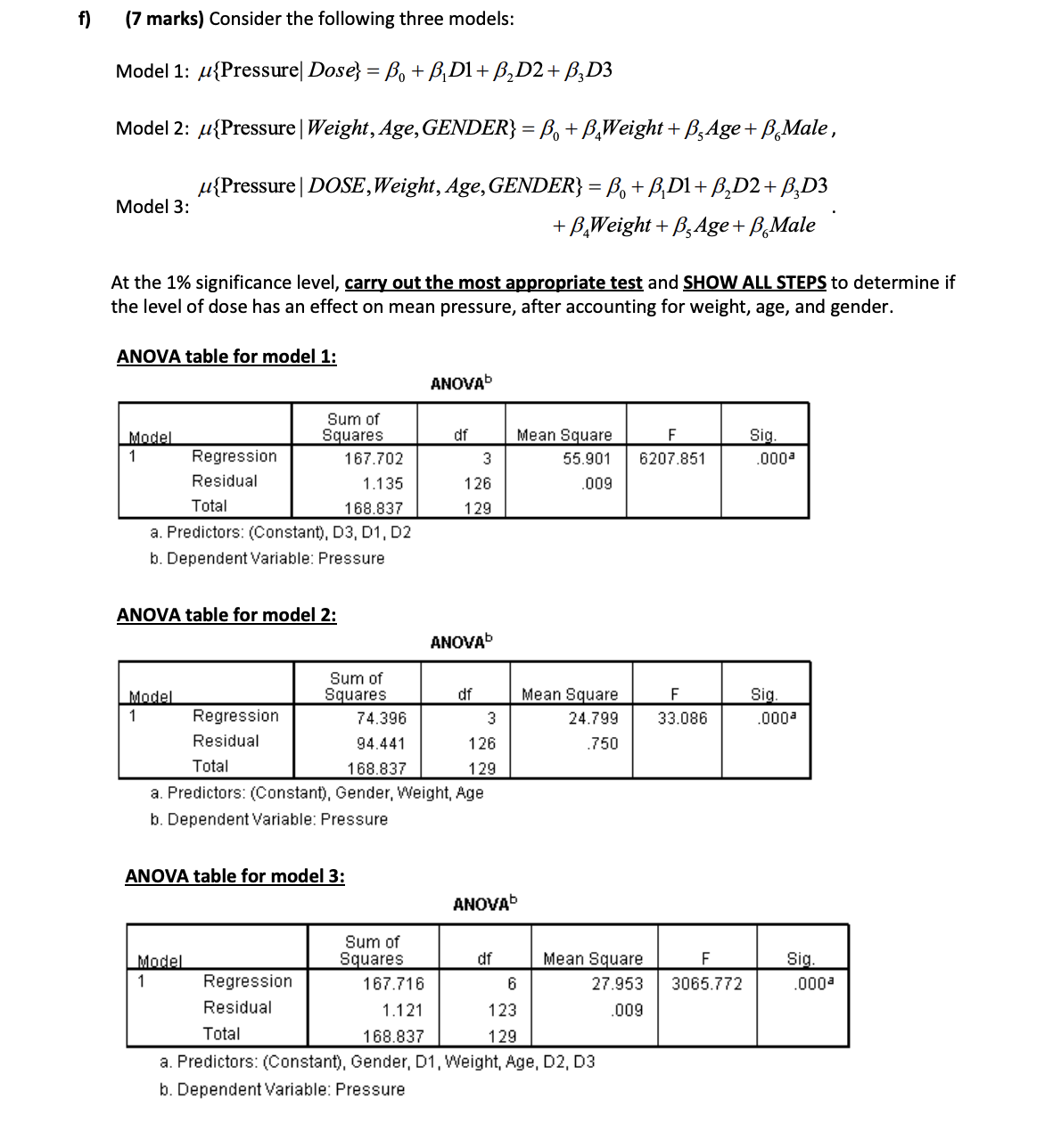
2. (Six parts; 22 marks in total) Persistent patent ductus arteriosus (PDA) is a medical condition that affects many very low-birth weight infants. Infants with PDA have an increased risk of serious ailment such as severe heart failure. The Apgar score is used to assess the health of an infant one minute after birth. The one-minute Apgar score measures how well the newborn tolerated the birthing process. A score of seven to 10 is normal and indicates the newborn is in good condition. Any score less than seven indicates that the baby needs assistance such as helping the infant breathe. Airway pressure is a measure of respiratory status, usually measured seven days after birth. Some researchers determined that early ibuprofen administration might prevent PDA in preterm neonates. A sample of 130 such infants was randomly divided into 4 groups. 32 were treated with one dose of ibuprofen, 33 with two doses, 33 with three doses, and 32 with a saline solution. The following is the description of variables under study. Variable Gender Dose Weight Age Score Pressure Description of Variables Male OR Female, Dose of ibuprofen (an integer from 0 to 3), Birth weight (in pounds), Gestational age (in weeks), One-minute Apgar score, Air-way pressure (in cm H2O) seven days after birth. Define variables Gender and Dose using the following indicator variables: male 1 for a Male and male = 0 for a Female, D1 = 1 if Dose of ibuprofen is 1 and D1 = 0 otherwise, D2 = 1 if Dose of ibuprofen is 2 and D2 = 0 otherwise, D3 = 1 if Dose of ibuprofen is 3 and D3 = 0 otherwise. Note: No output is needed for questions (a) to (c). Consider the following regression model with pressure as the response: {pressure | weight, GENDER, DOSE} = B + Bweight + male + D1 + D2 + D3 + B(weight male) + B(weight D1) + +B10 (weight maleD1) + B (weight This model will be referred to as the 'original' model. (weight D2) + B(weight D3) male D2) + B (weight x male xD3) f) (7 marks) Consider the following three models: Model 1: {Pressure| Dose} = B + D1 + D2+ D3 Model 2: {Pressure | Weight, Age, GENDER} = + Weight + BAge + B Male, Model 3: {Pressure | DOSE, Weight, Age, GENDER} = B + BD1 + D2 + D3 +B Weight + BAge + B Male At the 1% significance level, carry out the most appropriate test and SHOW ALL STEPS to determine if the level of dose has an effect on mean pressure, after accounting for weight, age, and gender. ANOVA table for model 1: Model 1 Regression Residual Total ANOVA Sum of Squares df 167.702 3 1.135 126 Mean Square 55.901 .009 F Sig. 6207.851 .000 168.837 129 a. Predictors: (Constant), D3, D1, D2 b. Dependent Variable: Pressure ANOVA table for model 2: ANOVAb Model Sum of Squares df 1 Regression 74.396 Residual 94.441 3 126 Mean Square 24.799 .750 F 33.086 Sig. .000a Total 168.837 129 a. Predictors: (Constant), Gender, Weight, Age b. Dependent Variable: Pressure ANOVA table for model 3: Model 1 Regression Residual Total ANOVA Sum of Squares df Mean Square 167.716 6 27.953 F 3065.772 Sig. .000a 1.121 123 .009 168.837 129 a. Predictors: (Constant), Gender, D1, Weight, Age, D2, D3 b. Dependent Variable: Pressure