Answered step by step
Verified Expert Solution
Question
1 Approved Answer
2. Suppose at t=0 a certain amount of inert solute A is released at the plane x=0 (for e.g. solute injected carefully into a column
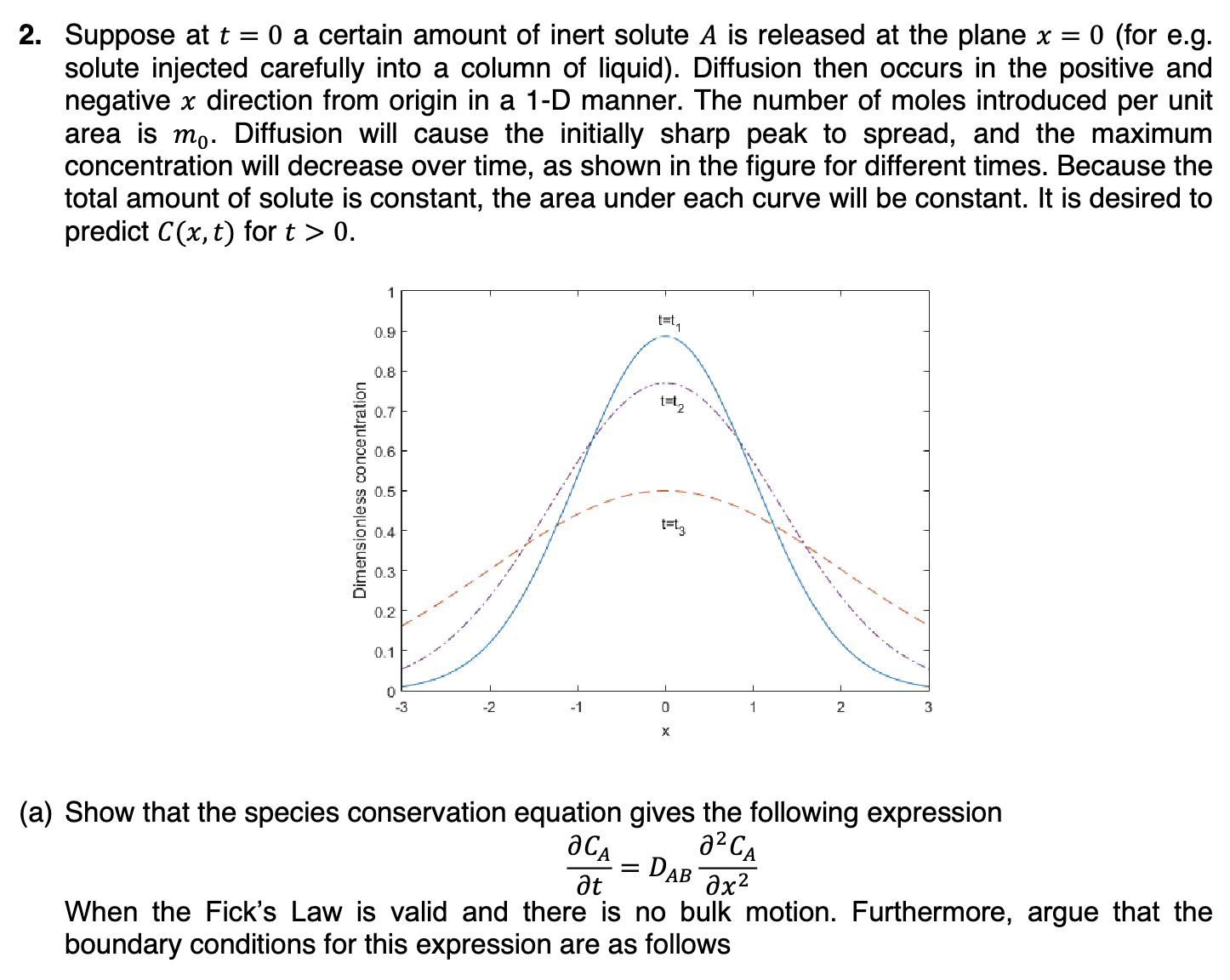
 2. Suppose at t=0 a certain amount of inert solute A is released at the plane x=0 (for e.g. solute injected carefully into a column of liquid). Diffusion then occurs in the positive and negative x direction from origin in a 1-D manner. The number of moles introduced per unit area is m0. Diffusion will cause the initially sharp peak to spread, and the maximum concentration will decrease over time, as shown in the figure for different times. Because the total amount of solute is constant, the area under each curve will be constant. It is desired to predict C(x,t) for t>0. (a) Show that the species conservation equation gives the following expression tCA=DABx22CA When the Fick's Law is valid and there is no bulk motion. Furthermore, argue that the boundary conditions for this expression are as follows CA(,t)=0;xCA(0,t)=0;2m0=0CA(x,t)dx (b) The given problem does not have a definite length scale and it is possible to solve this problem using the similarity method and the following variables: =2(DABt)1/2x,()=t1/2CA(x,t) Here is the dimensionless similarity variable and represents the scaled concentration. Using the above variables show that the governing equation reduces to d2d2+2dd+2=dd(dd+2)=0 (c) Solve the equation using the above boundary conditions and substitute and to arrive at the following expression: CA(x,t)=2(DABt)1/2m0ex2/4DABt
2. Suppose at t=0 a certain amount of inert solute A is released at the plane x=0 (for e.g. solute injected carefully into a column of liquid). Diffusion then occurs in the positive and negative x direction from origin in a 1-D manner. The number of moles introduced per unit area is m0. Diffusion will cause the initially sharp peak to spread, and the maximum concentration will decrease over time, as shown in the figure for different times. Because the total amount of solute is constant, the area under each curve will be constant. It is desired to predict C(x,t) for t>0. (a) Show that the species conservation equation gives the following expression tCA=DABx22CA When the Fick's Law is valid and there is no bulk motion. Furthermore, argue that the boundary conditions for this expression are as follows CA(,t)=0;xCA(0,t)=0;2m0=0CA(x,t)dx (b) The given problem does not have a definite length scale and it is possible to solve this problem using the similarity method and the following variables: =2(DABt)1/2x,()=t1/2CA(x,t) Here is the dimensionless similarity variable and represents the scaled concentration. Using the above variables show that the governing equation reduces to d2d2+2dd+2=dd(dd+2)=0 (c) Solve the equation using the above boundary conditions and substitute and to arrive at the following expression: CA(x,t)=2(DABt)1/2m0ex2/4DABt Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


