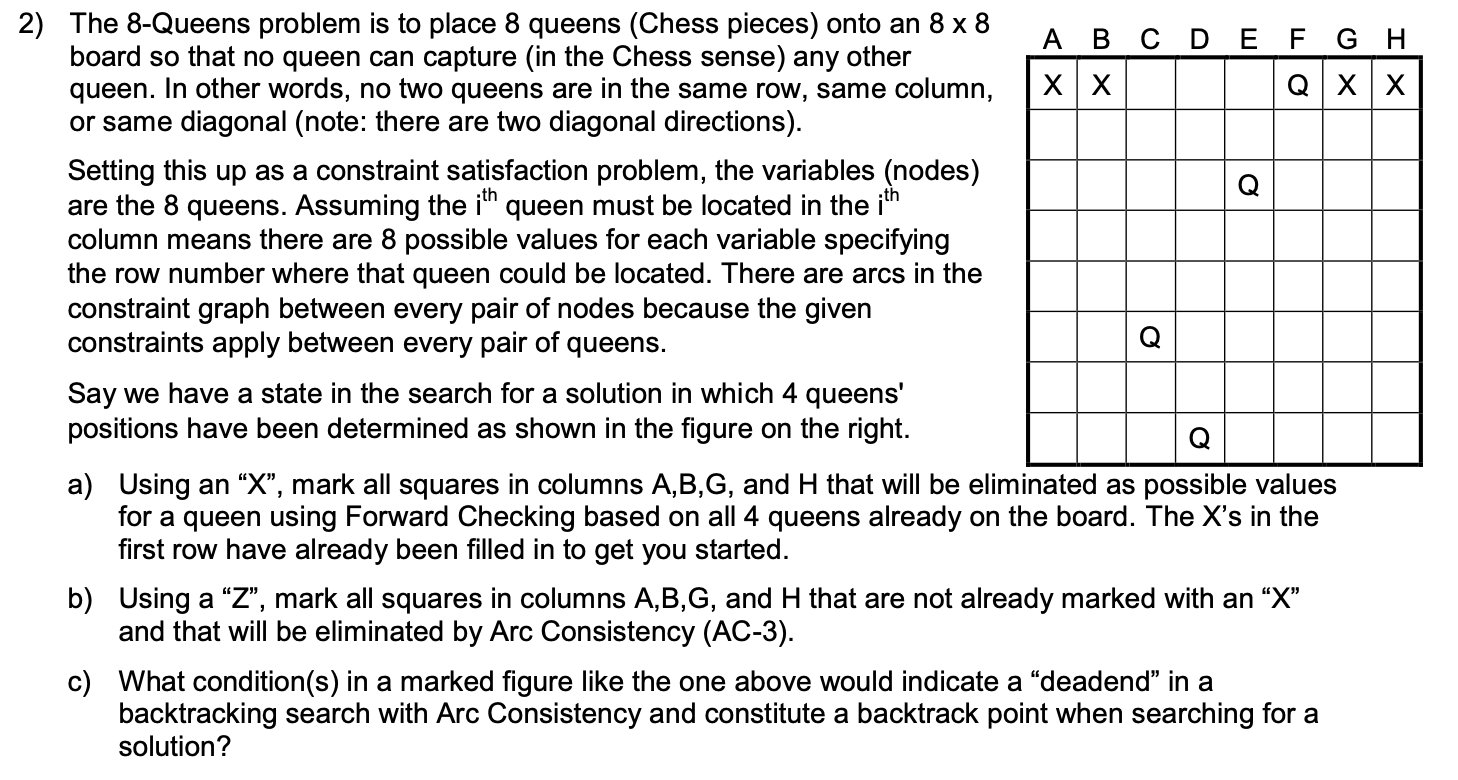
2) The 8-Queens problem is to place 8 queens (Chess pieces) onto an 8 x 8 A B C D E F G H board so that no queen can capture (in the Chess sense) any other queen. In other words, no two queens are in the same row, same column, XX Q|XX or same diagonal (note: there are two diagonal directions). Setting this up as a constraint satisfaction problem, the variables (nodes) are the 8 queens. Assuming the ith queen must be located in the ith column means there are 8 possible values for each variable specifying the row number where that queen could be located. There are arcs in the constraint graph between every pair of nodes because the given constraints apply between every pair of queens. Say we have a state in the search for a solution in which 4 queens' positions have been determined as shown in the figure on the right. Q a) Using an X, mark all squares in columns A,B,G, and H that will be eliminated as possible values for a queen using Forward Checking based on all 4 queens already on the board. The X's in the first row have already been filled in to get you started. b) Using a Z, mark all squares in columns A,B,G, and H that are not already marked with an X and that will be eliminated by Arc Consistency (AC-3). c) What condition(s) in a marked figure like the one above would indicate a deadend in a backtracking search with Arc Consistency and constitute a backtrack point when searching for a solution? 2) The 8-Queens problem is to place 8 queens (Chess pieces) onto an 8 x 8 A B C D E F G H board so that no queen can capture (in the Chess sense) any other queen. In other words, no two queens are in the same row, same column, XX Q|XX or same diagonal (note: there are two diagonal directions). Setting this up as a constraint satisfaction problem, the variables (nodes) are the 8 queens. Assuming the ith queen must be located in the ith column means there are 8 possible values for each variable specifying the row number where that queen could be located. There are arcs in the constraint graph between every pair of nodes because the given constraints apply between every pair of queens. Say we have a state in the search for a solution in which 4 queens' positions have been determined as shown in the figure on the right. Q a) Using an X, mark all squares in columns A,B,G, and H that will be eliminated as possible values for a queen using Forward Checking based on all 4 queens already on the board. The X's in the first row have already been filled in to get you started. b) Using a Z, mark all squares in columns A,B,G, and H that are not already marked with an X and that will be eliminated by Arc Consistency (AC-3). c) What condition(s) in a marked figure like the one above would indicate a deadend in a backtracking search with Arc Consistency and constitute a backtrack point when searching for a solution