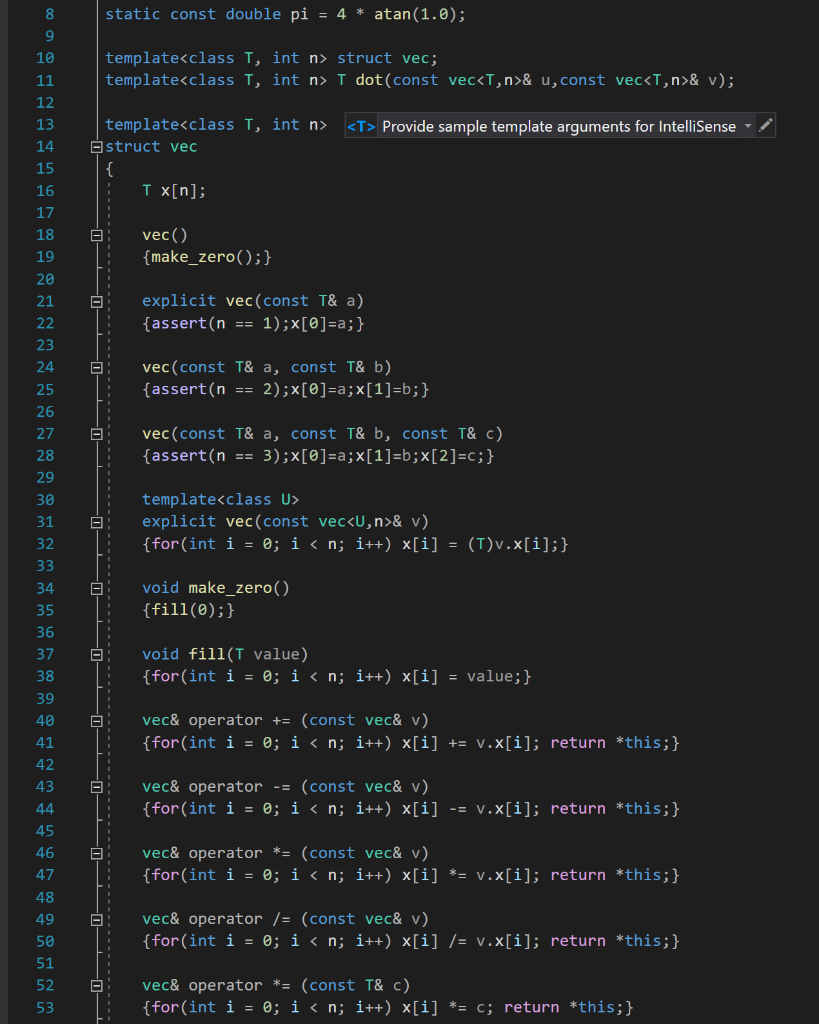
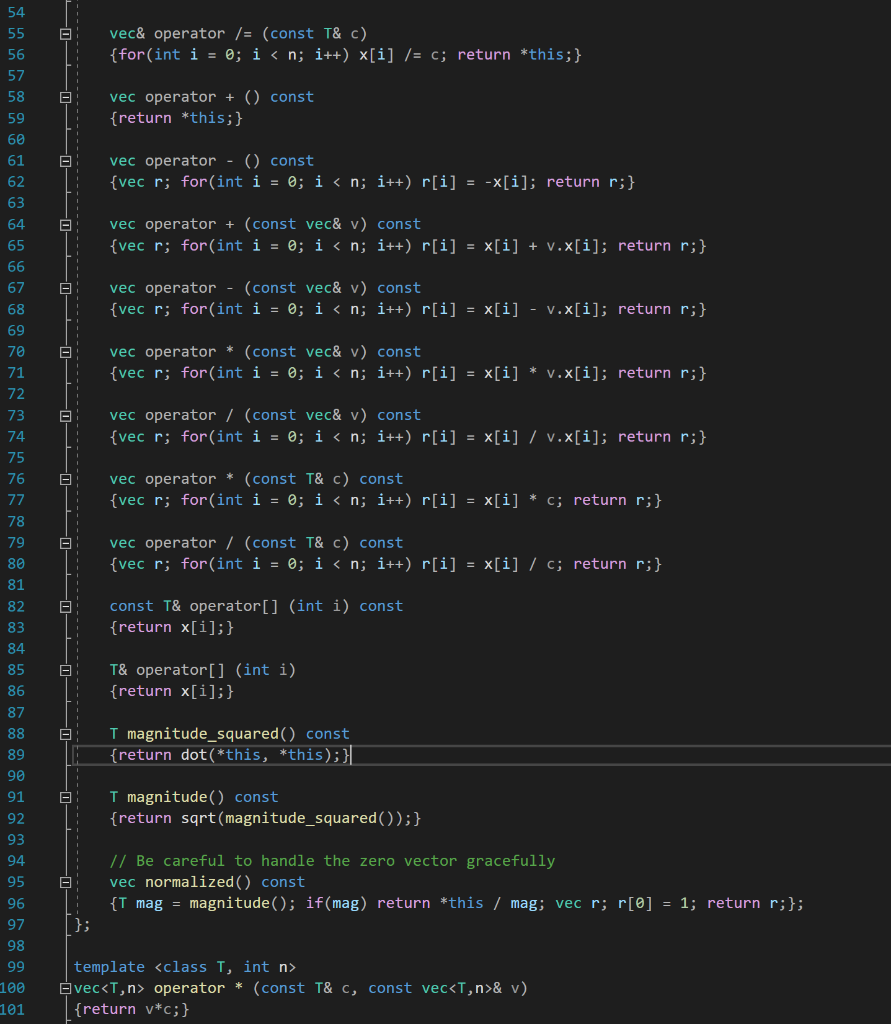
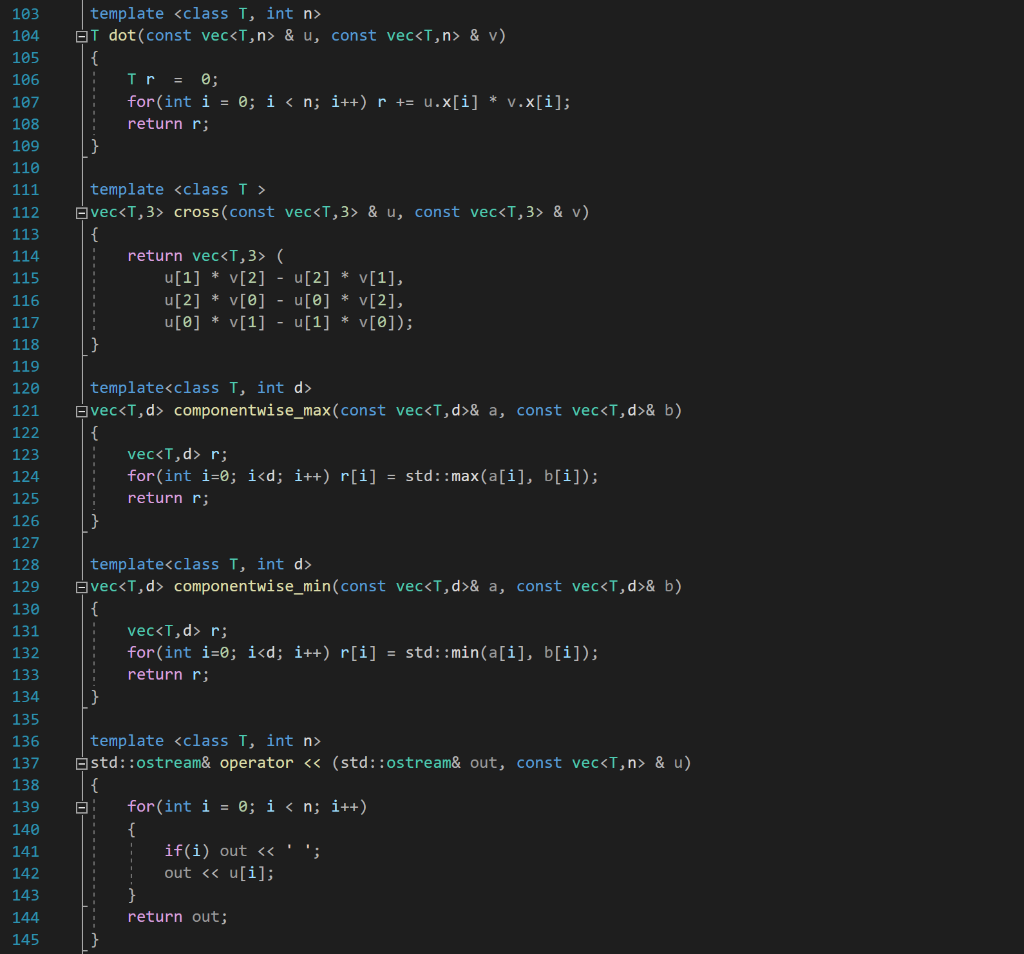
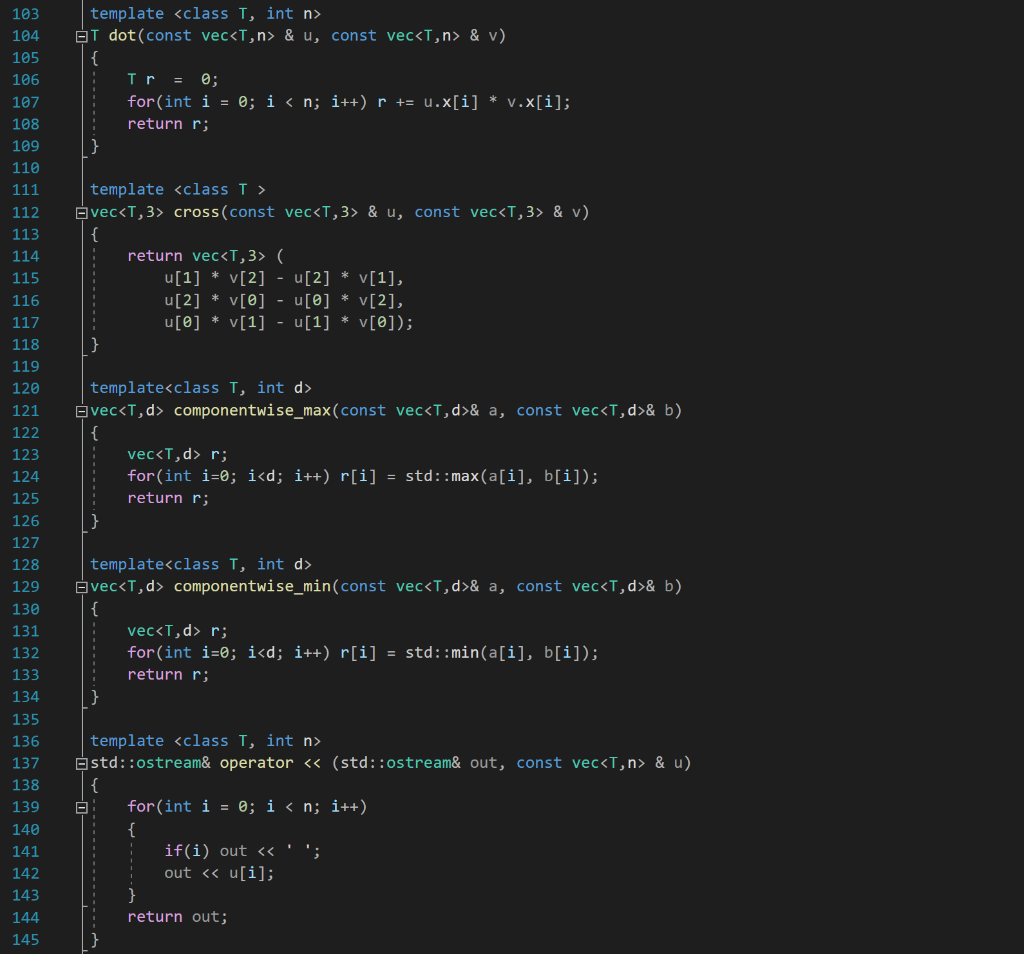
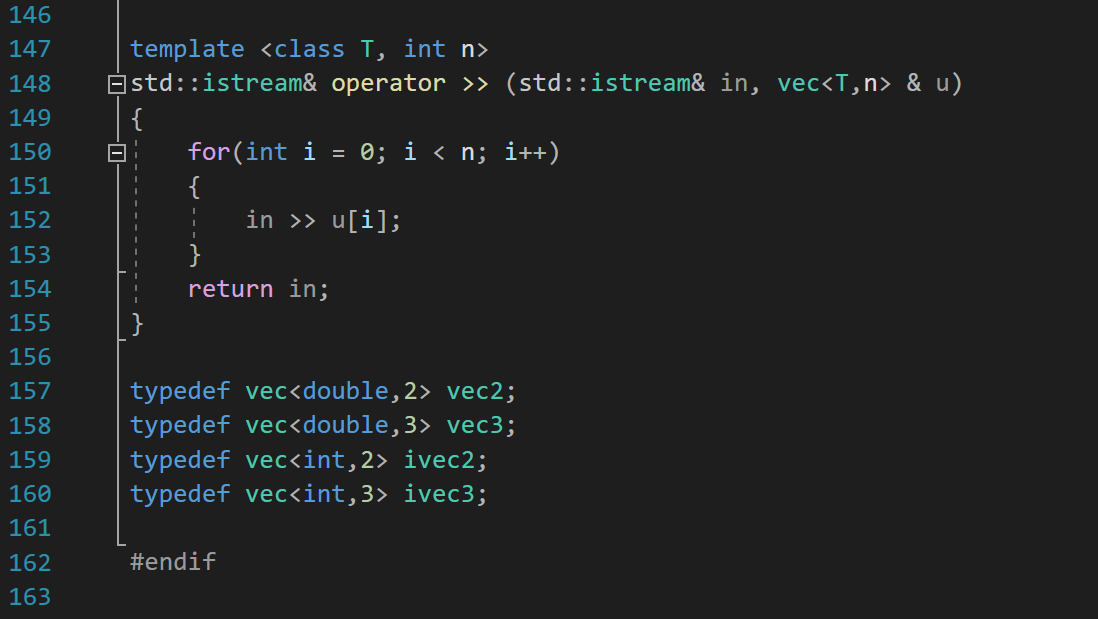
2. Write C++ code using vec.h to accomplish each of these tasks. You may assume that u, v, and w are of type vec3 and that a and b are scalars of type double. (a) u = (2,3,5) (b) w = u 3 +-V a b (C) w = 3u x v (d) Normalize u in place. (e) w = (|| _|| +1)v. (f) a = 1 -u.V (g) a = uo (get the first entry from the vector) 8 9 static const double pi = 4 * atan(1.0); 10 template struct vec; template T dot(const vec& u,const vec& v); Provide sample template arguments for IntelliSense template struct vec { T x[n]; 11 12 13 14 15 16 17 18 19 20 21 22 23 24 vec() {make_zero();} explicit vec(const T& a) {assert(n == 1);x[0]=a;} vec(const T& a, const T& b) {assert(n == 2);x[@]=a;x[1]=b;} vec(const T& a, const T& b, const T& c) {assert(n == 3);x[0]=a;x[1]=b;x[2]=c;} 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 template explicit vec(const vec& v) {for(int i = 0; i vec operator * (const T& c, const vec& v) {return v*c;} template T dot(const vec & u, const vec & v) { Ir = 0; for(int i = 0; i vec cross(const vec & u, const vec & v) { return vec ( u[1] * V[2] - u[2] * V[1], u[2] * V[@] - u[0] * V[2], u[@] * V[1] - u[1] * V[0]); } 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 template vec componentwise_max(const vec& a, const vec& b) { vec r; for(int i=0; i vec componentwise_min(const vec& a, const vec& b) { vec r; for(int i=0; i std::ostream& operator (std::ostream& out, const vec & u) { - for(int i = 0; i T dot(const vec & u, const vec & v) { Ir = 0; for(int i = 0; i vec cross(const vec & u, const vec & v) { return vec ( u[1] * V[2] - u[2] * V[1], u[2] * V[@] - u[0] * V[2], u[@] * V[1] - u[1] * V[0]); } 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 template vec componentwise_max(const vec& a, const vec& b) { vec r; for(int i=0; i vec componentwise_min(const vec& a, const vec& b) { vec r; for(int i=0; i std::ostream& operator (std::ostream& out, const vec & u) { - for(int i = 0; i std::istream& operator > (std::istream& in, vec & u) { for(int i = 0; i > u[i]; } return in; I 158 159 160 161 typedef vec vec2; typedef vec double,3> vec3; typedef vec ivec2; typedef vec ivec3; #endif 162 163 2. Write C++ code using vec.h to accomplish each of these tasks. You may assume that u, v, and w are of type vec3 and that a and b are scalars of type double. (a) u = (2,3,5) (b) w = u 3 +-V a b (C) w = 3u x v (d) Normalize u in place. (e) w = (|| _|| +1)v. (f) a = 1 -u.V (g) a = uo (get the first entry from the vector) 8 9 static const double pi = 4 * atan(1.0); 10 template struct vec; template T dot(const vec& u,const vec& v); Provide sample template arguments for IntelliSense template struct vec { T x[n]; 11 12 13 14 15 16 17 18 19 20 21 22 23 24 vec() {make_zero();} explicit vec(const T& a) {assert(n == 1);x[0]=a;} vec(const T& a, const T& b) {assert(n == 2);x[@]=a;x[1]=b;} vec(const T& a, const T& b, const T& c) {assert(n == 3);x[0]=a;x[1]=b;x[2]=c;} 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 template explicit vec(const vec& v) {for(int i = 0; i vec operator * (const T& c, const vec& v) {return v*c;} template T dot(const vec & u, const vec & v) { Ir = 0; for(int i = 0; i vec cross(const vec & u, const vec & v) { return vec ( u[1] * V[2] - u[2] * V[1], u[2] * V[@] - u[0] * V[2], u[@] * V[1] - u[1] * V[0]); } 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 template vec componentwise_max(const vec& a, const vec& b) { vec r; for(int i=0; i vec componentwise_min(const vec& a, const vec& b) { vec r; for(int i=0; i std::ostream& operator (std::ostream& out, const vec & u) { - for(int i = 0; i T dot(const vec & u, const vec & v) { Ir = 0; for(int i = 0; i vec cross(const vec & u, const vec & v) { return vec ( u[1] * V[2] - u[2] * V[1], u[2] * V[@] - u[0] * V[2], u[@] * V[1] - u[1] * V[0]); } 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 template vec componentwise_max(const vec& a, const vec& b) { vec r; for(int i=0; i vec componentwise_min(const vec& a, const vec& b) { vec r; for(int i=0; i std::ostream& operator (std::ostream& out, const vec & u) { - for(int i = 0; i std::istream& operator > (std::istream& in, vec & u) { for(int i = 0; i > u[i]; } return in; I 158 159 160 161 typedef vec vec2; typedef vec double,3> vec3; typedef vec ivec2; typedef vec ivec3; #endif 162 163<><><><><><><><><><>