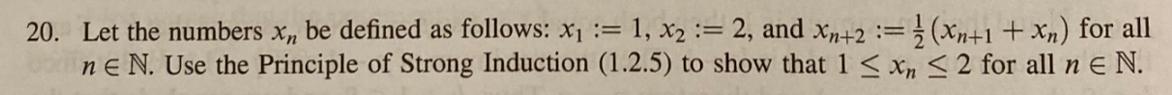
20. Let the numbers x,, be defined as follows: x=1, x = 2, and xn+2 = ne N. Use the Principle of Strong Induction (1.2.5) to show that 1 x (xn+1 + xn) for all 2 for all neN. 1.2.5 Principle of Strong Induction Let S be a subset of N such that (1") 1 S. (2") For every kEN, if {1, 2, ..., k} CS, then k +1ES. Then S=N.