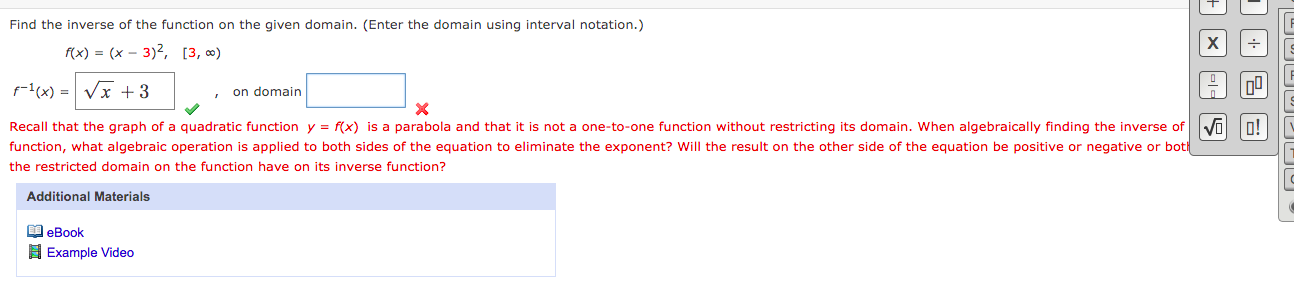
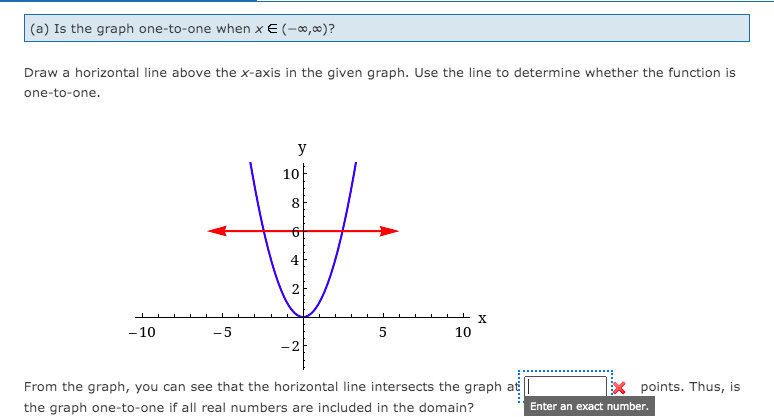
21.

Use a calculator to graph the function. Then, using the graph, give three points on the graph of the inverse with the y-coordinates given. f(x) = x3 + x - 5, y = 0, 1, 2 y =0 ( x, y) = y = 1 (x, y) = y = 2 ( x, y ) =Find the inverse of the function on the given domain. (Enter the domain using interval notation.) X f(x) = (x+ 6)2 - 7, [-6, 00) F-1 ( x) = Vx+7 - 6 on domain X Recall that the graph of a quadratic function is a parabola and that it is not a one-to-one function without restricting its domain. When algebraically finding the inverse of a quadrat VO 0! algebraic operation is applied to both sides of the equation to eliminate the exponent of an isolated term? Will the result on the other side of the equation after the exponent is elim negative or both? What affect does the restricted domain on the function have on its inverse function? Additional MaterialsFind the Inverse of the Function on the given domain. (Enter the domain using interval notation.) For) - (x 3):. [3. on) f'l(x) - \\E + 3 , on domain |:| V X Recall that the gmph of a quadmtlc Jnctlun y - Rx) Is a parabola and that it is not a one-to-one function without restricting It: domain. When algebraically nding the Inverse of a a function, what algebraic operation is applied to both sides of the equation to eliminate the exponent? Will the result on the other side of the equation be positive or negative or bot the restricted domain on the function have on its inverse Function? @ eBonk I Example Video Find the inverse of the function. f(x) = 1 - 3 X F-1 (x) = , on domain (-co, co){a} Is the graph one-to-one when x E {m,m]? Draw a horizontal line above the x-axis in the given graph. Use the line to determine whether the function is one-to-one. From the graph, you can see that the horizontal line intersects the graph at _ ix points. Thus, is the graph one-to-one if all real numbers are included in the domain? ' Enter an exact number'- (c) Sketch the graph of the inverse function. Sketch the graph of the inverse function by reflecting the graph over the line y = x. If (x, y) is a point on the graph of f(x) then y,X is a point on the graph of f 1(x). Thus we can sketch the graph of f(x) by reflecting the graph of ((x) over the line y = X Choose the correct graph of the inverse function