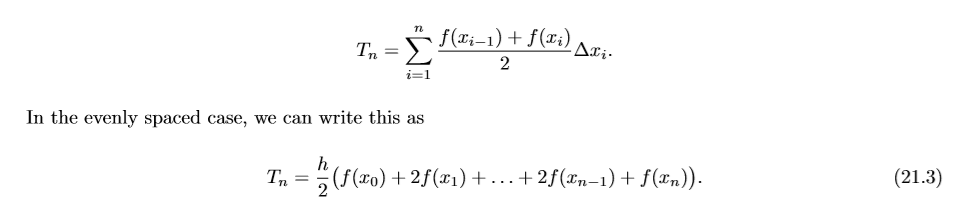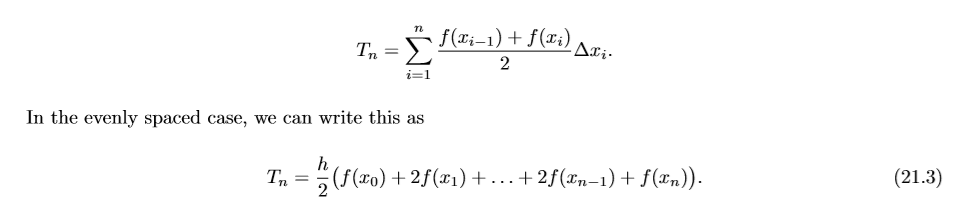
21.1 For the integral Vadr calculate L4, R4, and T4 with even spacing (by hand, but use a calculator and a lot of digits) using formulas (21.1), (21.2) and (21.3). Find the percentage error of these approximations, using the exact value. 21.2 Write a well-commented MATLAB function program myints whose inputs are f, a, b and n and whose outputs are L, R and T, the left, right and trapezoid integral approximations for f on [a, b] with n subintervals. To make it efficient, take advantage of the fact that Ar; is constant, use x = linspace(a,b,n+1) to make the x values, use y = f(x) to make the y values, use slice and sum to add the 2nd to nth y entries once, and then add on the missing terms to obtain the left, right and trapezoid approximations. Change to format long and apply your program to the integral i vadx. Compare with the results of the previous exercise. Also find L 100, R100 and T100 and the percentage errors of these approximations. Turn in the program and a brief summary of the results. Often we can take fri} to be evenly spaced, with each interval having the same width: h=67 n where n is the number of subintervals. If this is the case, then Ln and Rn simplify to n-1 In =h f(x) and (21.1) i= 0 Rn=hf(). (21.2) i=1 The foolishness of choosing left or right endpoints is illustrated in Figure 21.1. As you can see, for a very simple function like f()=1+.5.x, each rectangle of Ln is too short, while each rectangle of Rn is too tall. This will hold for any increasing function. For decreasing functions Ln will always be too large while Rn will always be too small. f(Ii-1) + f(xi) 22 In the evenly spaced case, we can write this as (20) + 2f (21) +...+2f (In-1) + f(n)). (21.3) 21.1 For the integral Vadr calculate L4, R4, and T4 with even spacing (by hand, but use a calculator and a lot of digits) using formulas (21.1), (21.2) and (21.3). Find the percentage error of these approximations, using the exact value. 21.2 Write a well-commented MATLAB function program myints whose inputs are f, a, b and n and whose outputs are L, R and T, the left, right and trapezoid integral approximations for f on [a, b] with n subintervals. To make it efficient, take advantage of the fact that Ar; is constant, use x = linspace(a,b,n+1) to make the x values, use y = f(x) to make the y values, use slice and sum to add the 2nd to nth y entries once, and then add on the missing terms to obtain the left, right and trapezoid approximations. Change to format long and apply your program to the integral i vadx. Compare with the results of the previous exercise. Also find L 100, R100 and T100 and the percentage errors of these approximations. Turn in the program and a brief summary of the results. Often we can take fri} to be evenly spaced, with each interval having the same width: h=67 n where n is the number of subintervals. If this is the case, then Ln and Rn simplify to n-1 In =h f(x) and (21.1) i= 0 Rn=hf(). (21.2) i=1 The foolishness of choosing left or right endpoints is illustrated in Figure 21.1. As you can see, for a very simple function like f()=1+.5.x, each rectangle of Ln is too short, while each rectangle of Rn is too tall. This will hold for any increasing function. For decreasing functions Ln will always be too large while Rn will always be too small. f(Ii-1) + f(xi) 22 In the evenly spaced case, we can write this as (20) + 2f (21) +...+2f (In-1) + f(n)). (21.3)