Answered step by step
Verified Expert Solution
Question
1 Approved Answer
2A Calc Logarithmic Functions What you're Solving for Key: 6. Simplyfy the expression completly 7+14 Solve for x using logs 24 solve for t assume
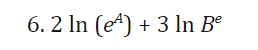
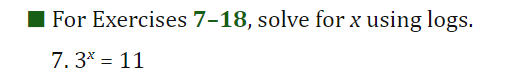
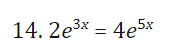
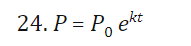
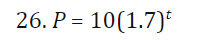
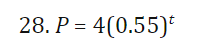
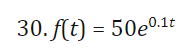
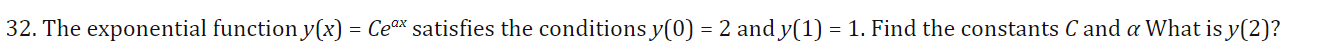
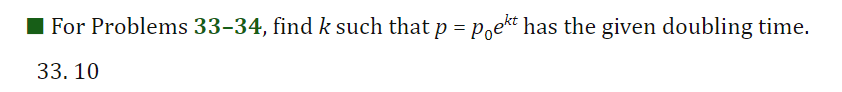
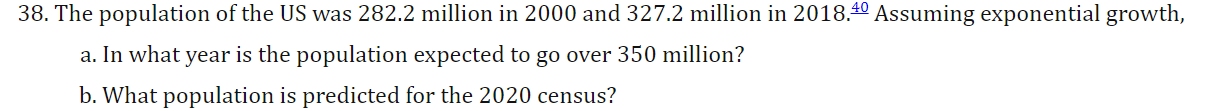

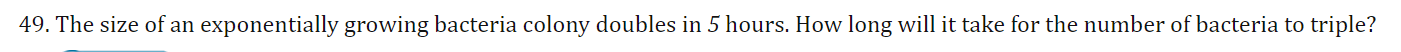

2A Calc Logarithmic Functions
What you're Solving for Key:
6. Simplyfy the expression completly
7+14 Solve for x using logs
24 solve for t assume a and b are are positve a and b =/ 1 and k is non zero (slash is supposed to be through the equal sign)
26+28 put functions in the form p=p0^e^kt
30 find the inverse
33 find k such that p=p0^e^kt
***PLEASE SHOW ALL WORK****
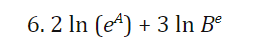
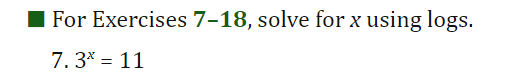
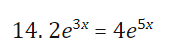
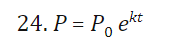
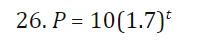
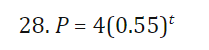
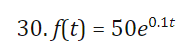
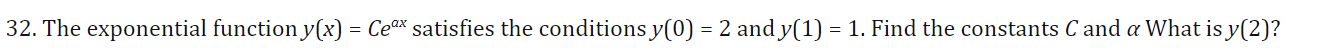
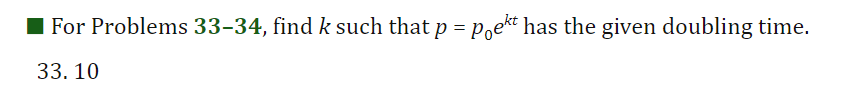
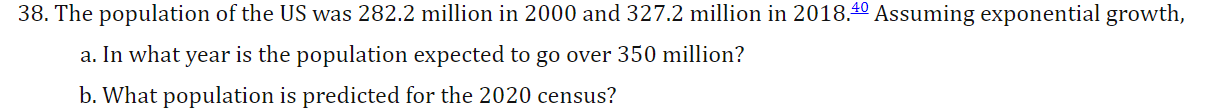

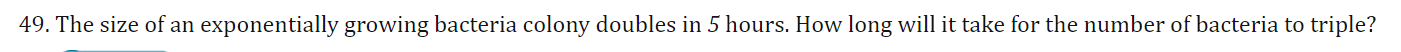

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


