3. (25 pts) Consider the par yield curve for the U.S. Treasury securities given in the table below (only the first 3 years of the curve are provided). Calculate the missing spot rates indicated by ???? using bootstrapping and add them to the table. (The example of bootstrapping given in the Chapter 10 slides will be very helpful in completing this table.) Show your work for all calculations in the space below the table

Year	Yield to Maturity (%)	Spot Rate (%)
0.5	5.25	5.25
1.0	5.50	5.50
1.5	5.75	????
2.0	6.00	????
2.5	6.25	????
3.0	6.50	????

I have added example picture below.

All prices and interest rates must be expressed to three decimal places. SHOW YOUR WORK FOR EVERY PROBLEM IN ORDER TO RECEIVE ANY CREDIT.

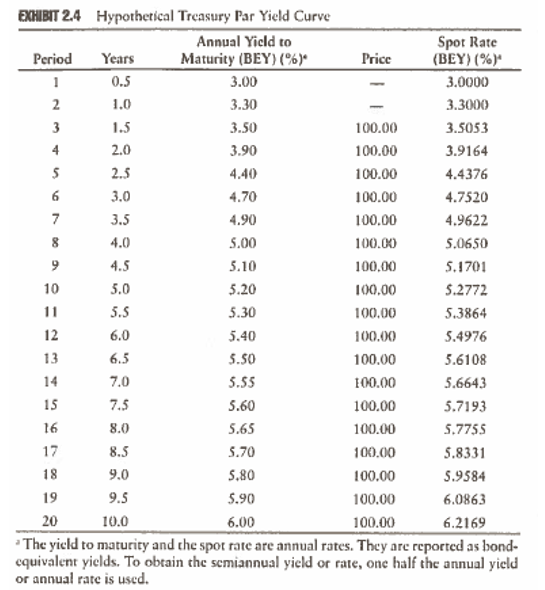
Example: we will bootstrap the spot rate for period 3 of the 1.5 year coupon bond. This is 23. We know that 21 = 3.00 and Z2 = 3.30 from Exhibit 2.4. They are given. These are annualized values and must be converted to semiannual values for calculation. From column 3 in Exhibit 2.4 on a previous slide, the annualized yield to maturity (coupon rate) for this bond is 3.50%. This means that the semiannual coupon is half of that, or 1.75% The bond is a semiannual bond with a tenor of 1.5 years, so there are three coupons re Bootstrapping the 1.5 year spot rate repayment of PAR simultaneous with the third coupon. The present value of the cash flows is then 1.75 1.75 101.75 100 = (1+z)(1+2,)? (1+z) where + -- 2, = one-half the annualized 6-month theoretical spot rate 2. = one-half the 1-year theoretical spot rate 2, = one-half the 1.5-year theoretical spot rate Since the 6-month spot rate is 3% and the 1-year spot rate is 3.30%, we know that 2, = 0.0150 and 2, = 0.0165 We can compute the present value of the 1.5-year coupon Treasury security as 1.75 1.75 101.75 1.75 1.75 101.75 100 {1+2,)*(1+2,)** 1+2,1 (1.0151' * (1.0165)2 * (1+27) Since the price of the 1.5-year coupon Treasury security is equal to its par value (see Exhibit 5), the following relationship must hold: 1.75 1.75 101.75 = 100 (1.015)'' (1.0165)2 (1+2) + + 101.75 1.7241+1.6936+ = 100 (1+ 2,1 101.75 = 96.5822 (1+2) 101.75 (1 + 2,1 96.5822 (1 +23) = 1.05351 2, = 0.017527 = 1.7527% Doubling this yield we obtain the bond-equivalent yield of 3.5053%, which is the theoretical 1.5-year spot rate. This is the rate that the market would apply to a 1.5-year zero-coupon Treasury security if, in fact, such a security existed. In other words, all Treasury cash flows to be received 1.5 years from now should be valued (i.e., discounted) ar 3.5053%. 4 2.5 EXHIBIT 24 Hypothetical Treasury Par Yield Curve Annual Yield to Spot Rate Period Years Maturity (BEY)()* Price (BEY) (%) 1 0.5 3.00 3.0000 2 1.0 3.30 3.3000 3 1.5 3.50 100.00 3.5053 2.0 3.90 100.00 3.9164 5 4.40 100.00 4.4376 6 3.0 4.70 100.00 4.7520 7 3.5 4.90 100,00 4.9622 8 4.0 5.00 100.00 5.0650 9 4.5 5.10 100.00 5.1701 10 5.0 5.20 100.00 5.2772 11 5.5 5.30 100,00 5.3864 12 6.0 5.40 100.00 5.4976 13 5.50 100.00 5.6108 14 5.55 100.00 5.6643 15 7.5 5.60 100.00 5.7193 16 8.0 5.65 100.00 5.7755 17 8.5 5.70 100.00 5.8331 18 9.0 5.80 100.00 5.9584 19 9.5 5.90 100.00 6.0863 10.0 6.00 100.00 6.2169 The yield to maturity and the spot rate are annual rates. They are reported as bond- cquivalent yields. To obtain the semiannual yield or rate, one half the annual yield or annual rate is used. 6.5 7.0 20 Example: we will bootstrap the spot rate for period 3 of the 1.5 year coupon bond. This is 23. We know that 21 = 3.00 and Z2 = 3.30 from Exhibit 2.4. They are given. These are annualized values and must be converted to semiannual values for calculation. From column 3 in Exhibit 2.4 on a previous slide, the annualized yield to maturity (coupon rate) for this bond is 3.50%. This means that the semiannual coupon is half of that, or 1.75% The bond is a semiannual bond with a tenor of 1.5 years, so there are three coupons re Bootstrapping the 1.5 year spot rate repayment of PAR simultaneous with the third coupon. The present value of the cash flows is then 1.75 1.75 101.75 100 = (1+z)(1+2,)? (1+z) where + -- 2, = one-half the annualized 6-month theoretical spot rate 2. = one-half the 1-year theoretical spot rate 2, = one-half the 1.5-year theoretical spot rate Since the 6-month spot rate is 3% and the 1-year spot rate is 3.30%, we know that 2, = 0.0150 and 2, = 0.0165 We can compute the present value of the 1.5-year coupon Treasury security as 1.75 1.75 101.75 1.75 1.75 101.75 100 {1+2,)*(1+2,)** 1+2,1 (1.0151' * (1.0165)2 * (1+27) Since the price of the 1.5-year coupon Treasury security is equal to its par value (see Exhibit 5), the following relationship must hold: 1.75 1.75 101.75 = 100 (1.015)'' (1.0165)2 (1+2) + + 101.75 1.7241+1.6936+ = 100 (1+ 2,1 101.75 = 96.5822 (1+2) 101.75 (1 + 2,1 96.5822 (1 +23) = 1.05351 2, = 0.017527 = 1.7527% Doubling this yield we obtain the bond-equivalent yield of 3.5053%, which is the theoretical 1.5-year spot rate. This is the rate that the market would apply to a 1.5-year zero-coupon Treasury security if, in fact, such a security existed. In other words, all Treasury cash flows to be received 1.5 years from now should be valued (i.e., discounted) ar 3.5053%. 4 2.5 EXHIBIT 24 Hypothetical Treasury Par Yield Curve Annual Yield to Spot Rate Period Years Maturity (BEY)()* Price (BEY) (%) 1 0.5 3.00 3.0000 2 1.0 3.30 3.3000 3 1.5 3.50 100.00 3.5053 2.0 3.90 100.00 3.9164 5 4.40 100.00 4.4376 6 3.0 4.70 100.00 4.7520 7 3.5 4.90 100,00 4.9622 8 4.0 5.00 100.00 5.0650 9 4.5 5.10 100.00 5.1701 10 5.0 5.20 100.00 5.2772 11 5.5 5.30 100,00 5.3864 12 6.0 5.40 100.00 5.4976 13 5.50 100.00 5.6108 14 5.55 100.00 5.6643 15 7.5 5.60 100.00 5.7193 16 8.0 5.65 100.00 5.7755 17 8.5 5.70 100.00 5.8331 18 9.0 5.80 100.00 5.9584 19 9.5 5.90 100.00 6.0863 10.0 6.00 100.00 6.2169 The yield to maturity and the spot rate are annual rates. They are reported as bond- cquivalent yields. To obtain the semiannual yield or rate, one half the annual yield or annual rate is used. 6.5 7.0 20