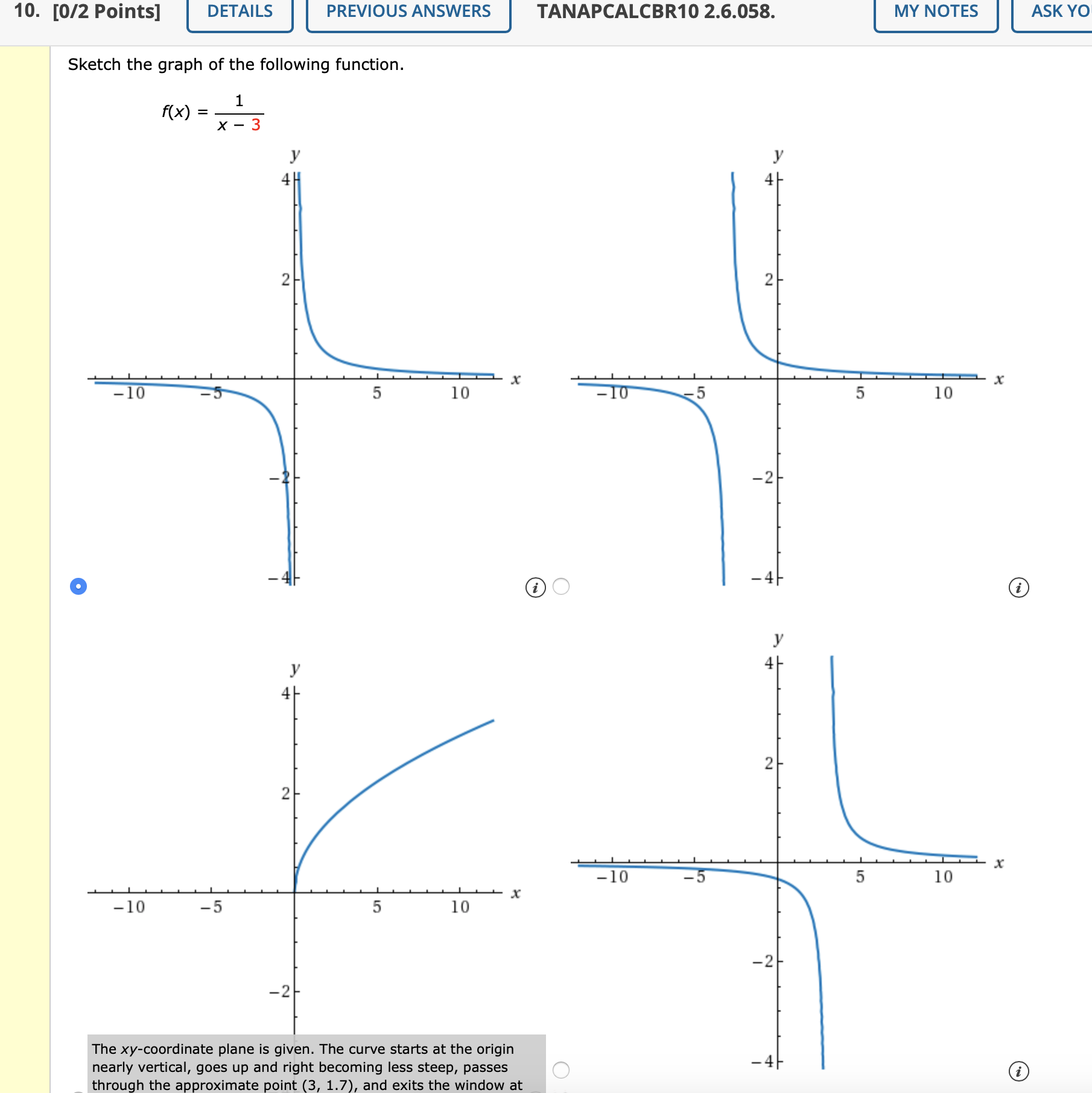
3. [-/4 Points] DETAILS TANAPCALCBR10 2.6.010. MY NOTES ASK YOUR T Use the four-step process to find the slope of the tangent line to the graph of the given function at any point. (Simplify your answers completely.) f (x) = -3 Step 1: f ( x + h ) = Step 2: f ( x + h) - f(x ) = Step 3: f (x + h) - f(x) h Step 4: f'(x) = lim f ( x + h) - f(x ) = h -0 h Need Help? Read It Watch It Talk to a Tutor 4. [-/4 Points] DETAILS TANAPCALCBR10 2.6.012. MY NOTES ASK YOUR T Use the four-step process to find the slope of the tangent line to the graph of the given function at any point. (Simplify your answers completely.) f(x) = 3- 6x Step 1: f ( x + h ) = Step 2: ( x + h ) - f ( x ) = Step 3: f ( x + h) - f(x) n Step 4: f'(x) = lim f ( x + h ) - f(x ) h - 0 h5. [-/4 Points] DETAILS TANAPCALCBR10 2.6.014. MY NOTES ASK YOUR TEA Use the four-step process to find the slope of the tangent line to the graph of the given function at any point. (Simplify your answers completely.) f ( x ) = _ _ 10' * 2 Step 1: f ( x + h ) = Step 2: f ( x + h ) - f (x ) = Step 3: f ( x + h) - f(x) = h Step 4: f'(x) = lim f ( x + h) - f(x) h - 0 h = Need Help? Read It Watch It Talk to a Tutor 6. [-/4 Points] DETAILS TANAPCALCBR10 2.6.016.MI. MY NOTES ASK YOUR TEA Use the four-step process to find the slope of the tangent line to the graph of the given function at any point. (Simplify your answers completely.) f ( x ) = 2x2 + 7x Step 1: f ( x + h) = Step 2: f ( x + h) - f (x ) = Step 3: f ( x + h ) - f(x) = h Step 4: f'(x) = lim f( x + h) - f(x) h- 010. [0/2 Points] DETAILS PREVIOUS ANSWERS TANAPCALCBR10 2.6.058. MY NOTES ASK YO Sketch the graph of the following function. f ( x ) = - 1 X - 3 2- -10 5 10 -10 -5 5 10 -2- O 2 2 -10 -5 5 10 -10 -5 5 10 X -2 The xy-coordinate plane is given. The curve starts at the origin nearly vertical, goes up and right becoming less steep, passes through the approximate point (3, 1.7), and exits the window at ODescribe f(x) at X = 3. (Select all that apply.) (21 The function is not defined at the point X = 3. (21 The function does not have a derivative at x = 3. Q The tangent line is vertical at the point x = 3. Q The derivative is zero at the point x = 3. (21 The function is discontinuous at the point x = 3. X