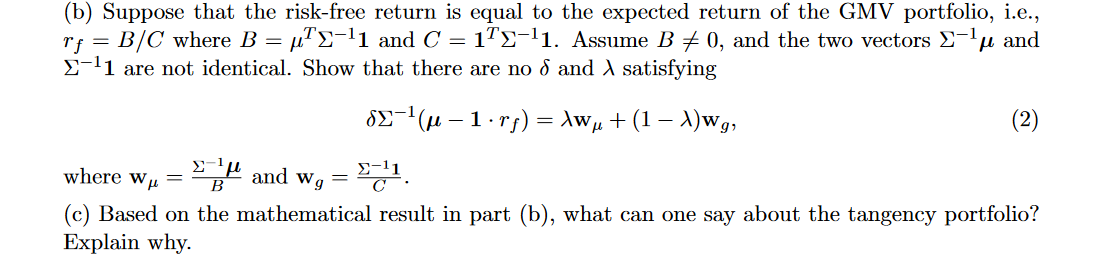3. (7pts) Consider the portfolio selection problem in a market with N(2) risky asset and one risk free asset that earns return rate rf. The expected returns of the risky assets are given by RN 1 and the covariance matrix of their returns is given by RNN. Assume is positive definite. Consider the problem {maxwRNs.t.{rf+wT(1rf)}wTw=p2, where rf+wT(1rf)=wT+(1wT1)rf is the expected return of the portfolio w. (a) Let p denote the expected return rate of the optimal portfolio for the above problem. Show ip=pprf[pcov(Ri,Rp)p], where Ri denotes the return rate of the i-th risky asset, and Rp is the return rate of the optimal portfolio. (b) Suppose that the risk-free return is equal to the expected return of the GMV portfolio, i.e., rf=B/C where B=T11 and C=1T11. Assume B=0, and the two vectors 1 and 11 are not identical. Show that there are no and satisfying 1(1rf)=w+(1)wg, where w=B1 and wg=C11. (c) Based on the mathematical result in part (b), what can one say about the tangency portfolio? Explain why