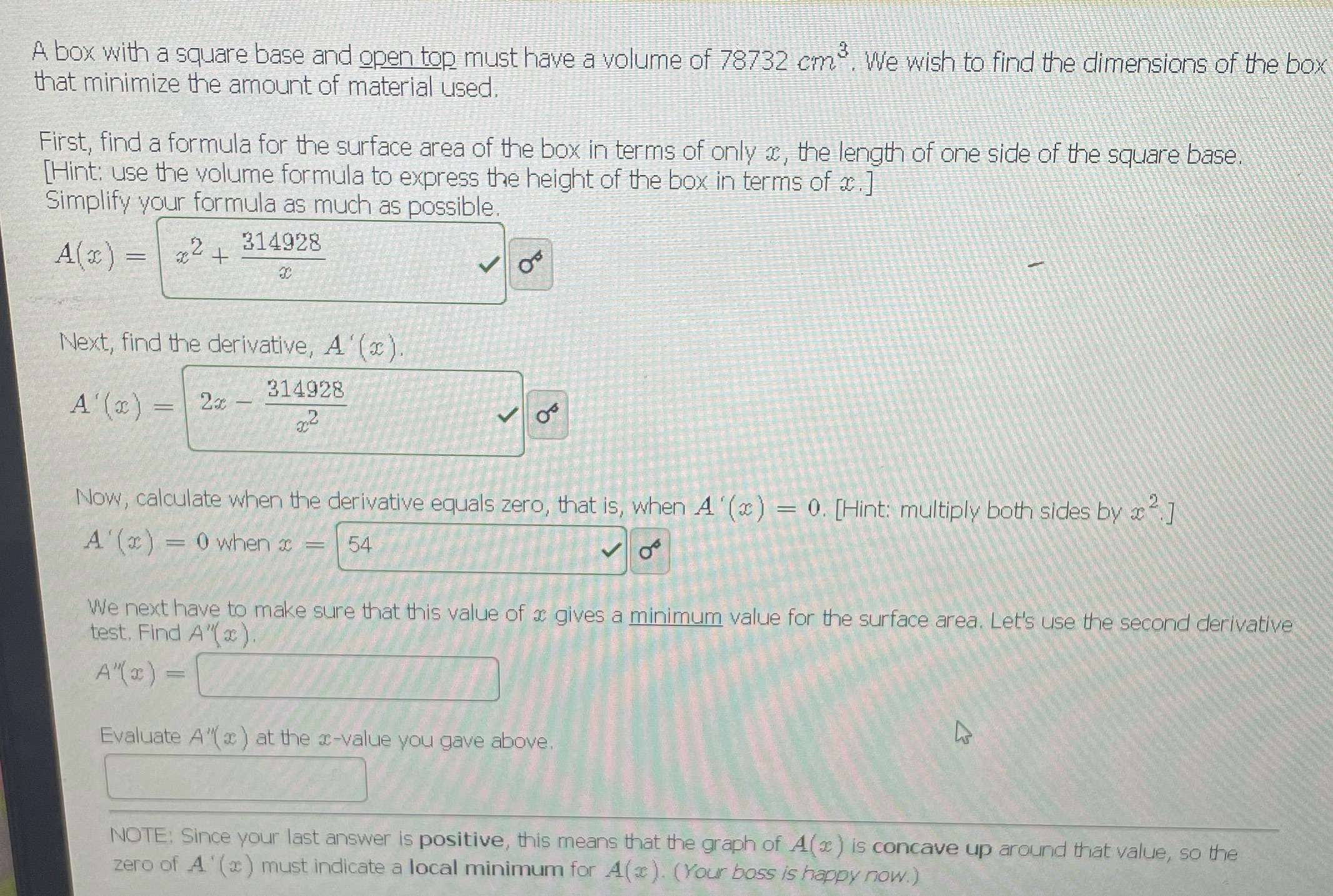
3 A box with a square base and open top must have a volume of 78732 cm. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only x, the length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of x.] Simplify your formula as much as possible. A(x) = x+ 2 314928 30 Next, find the derivative, A'(x). A'(x) = 2x 314928 32 00 Now, calculate when the derivative equals zero, that is, when A'(x) = 0. [Hint: multiply both sides by x2] A'(x) = 0 when x = 54 0 We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the second derivative test. Find A"). A"(x) = Evaluate A"(x) at the x-value you gave above. NOTE: Since your last answer is positive, this means that the graph of A(x) is concave up around that value, so the zero of A'(x) must indicate a local minimum for A(x). (Your boss is happy now.)