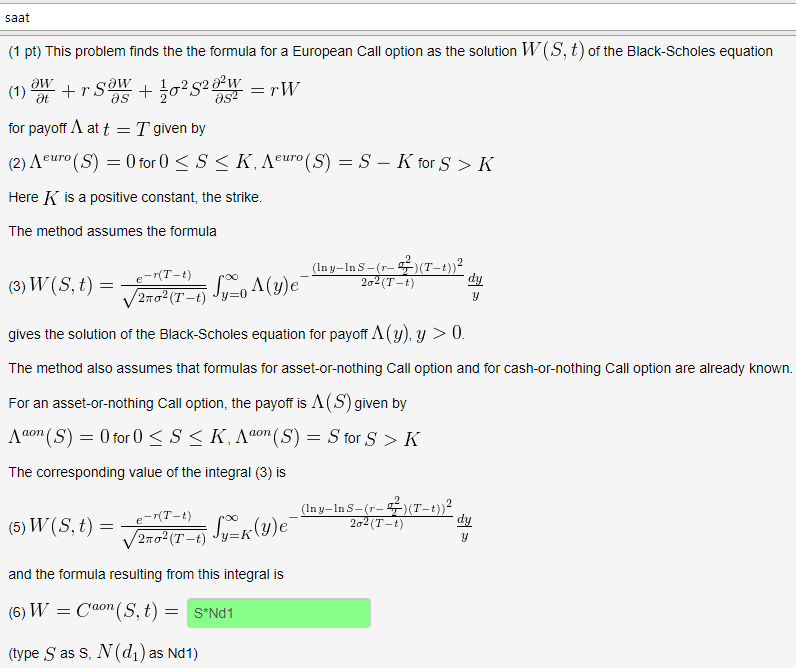
3. Consider a mass function dN/dM = M-1-x for x = 1.35 Assume there is some minimum Mass, Mmin = 0.1 Msun For some critical mass, Mc > Mmin, stars become black holes after the complete their main sequence evolution. Write down the algebraic formula for the fraction of stars which become black holes. If Mc = 20 Msun, what fraction of stars become black holes? Derive the Black-Scholes formula for the value of a European put option using the partial differential equation method. Let P(S,t) be the value of the European put. The boundary value problem for the European put is as follows: 1 Pt+ Pss+rSPs rP = 0, - S>0, 0 saat (1 pt) This problem finds the the formula for a European Call option as the solution W (S, t) of the Black-Scholes equation (1) aw t + r SW + o S W = rW as for payoff A at t = T given by (2) A euro (S) = 0 for 0 S K, Aeuro (S) = S K for S > K Here is a positive constant, the strike. The method assumes the formula (3) W (S,t) e-(T-t) = 20 (T-t) Syo (y)e (Iny-InS-(-)(T-t)) 202 (T-t) dy gives the solution of the Black-Scholes equation for payoff A(y), y > 0. The method also assumes that formulas for asset-or-nothing Call option and for cash-or-nothing Call option are already known. For an asset-or-nothing Call option, the payoff is A(S) given by Aaon (S) = 0 for 0 S K, Aon (S) = S for S > K The corresponding value of the integral (3) is (5) W (S,t) e-(T-t) = 2o (T-1) y=k(y)e (Iny-In S-(-)(T-t)) 202 (T-t) dy and the formula resulting from this integral is (6) W = Caon (S,t) = S*Nd1 (type S as S, N(d) as Nd1)