Question
3 friends are voting on a holiday destination. Each player chooses a destination to vote for, and the winner is the destination with the most
3 friends are voting on a holiday destination. Each player chooses a destination to vote for, and
the winner is the destination with the most votes. If all three are tied, then one destination is randomly
selected from the three, where each has a third probability of winning. The players of the game are
F1, F2 and F3, and fortunately for us, they all obey the von-Neuman-Morgenstern axioms. All three
rank a lottery which gives them their worst outcome with 20 percent chance and their best outcome
with 80 percent chance as equivalent to getting their second-best outcome with certainty. The ordinal
preferences of the holiday destinations Argentina, Bolivia and Columbia (A, B and C) are given by:
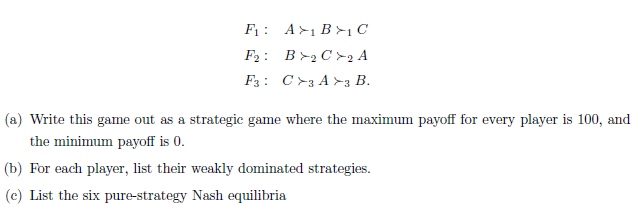
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


