Question
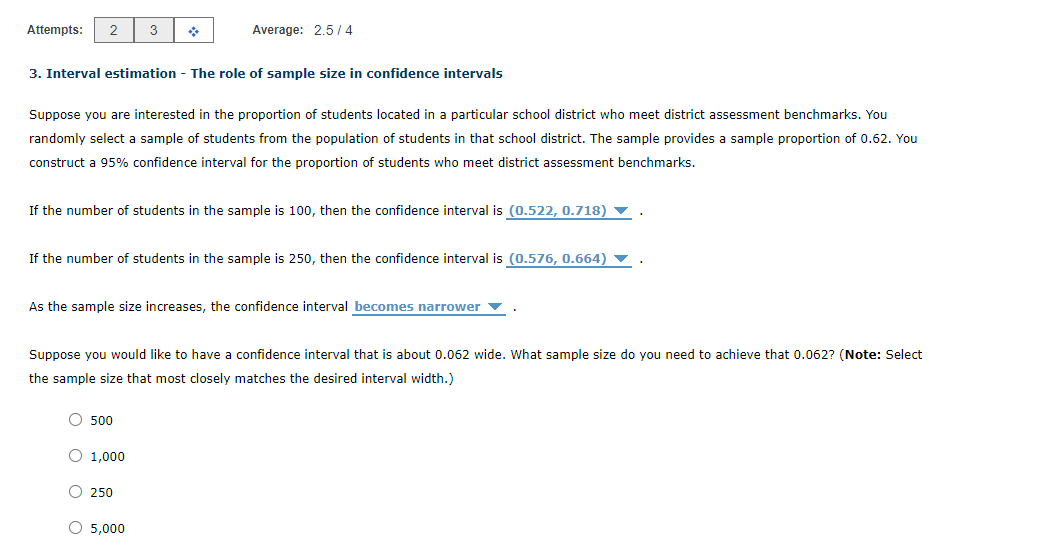
3. Interval estimation - The role of sample size in confidence intervals Suppose you are interested in the proportion of students located in a particular
3. Interval estimation - The role of sample size in confidence intervals
Suppose you are interested in the proportion of students located in a particular school district who meet district assessment benchmarks. You randomly select a sample of students from the population of students in that school district. The sample provides a sample proportion of 0.62. You construct a 95% confidence interval for the proportion of students who meet district assessment benchmarks.
If the number of students in the sample is 100, then the confidence interval is CHOICES ARE: (0.377, 0.722), (0.522, 0.718), (0.576, 0.664), (0.558, 0.682).
If the number of students in the sample is 250, then the confidence interval is CHOICES ARE: (0.522, 0.718), (0.558, 0.682) (0.576, 0.664), (0.417, 0.826) .
As the sample size increases, the confidence interval becomes CHOICES ARE: STAYS THE SAME, BECOMES WIDER, AND becomes narrower .
Suppose you would like to have a confidence interval that is about 0.062 wide. What sample size do you need to achieve that 0.062? (Note:Select the sample size that most closely matches the desired interval width. CHOOSE PLEASE
500
1,000
250
5,000
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


