3. Let (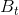) denote a Brownian motion under the real-world measure with 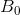= 0. Consider the Black-Scholes model for the stock price,

,

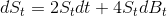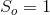
and the savings account is given by 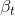= 1 for all t.

(a) Write down the condition for a portfolio in this model to be self-financing. Consider the portfolio given by 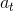= t (units of the stock) and 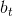= 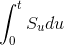(units of the savings account), determine with proof whether this portfolio is self-financing.

(b) State the Girsanov theorem. Using it, or otherwise, derive the expression (not the stochastic differential) for 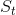, in terms of a Brownian motion under the equivalent martingale measure (EMM).

(c) Denote by 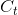the price at time t . Find the answer (in terms of the normal distribution function) for the case when t = 1.

BC B4 BC B4