Question: (3) Let (fn)neN be a sequence in C(0, 1) and (a)keN a sequence of positive numbers, such that the series E1 9k a converges

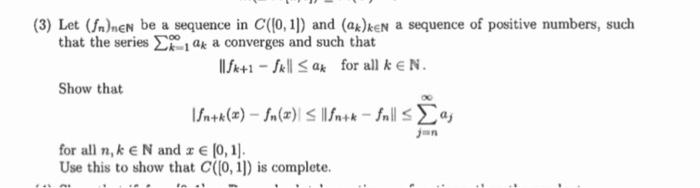
(3) Let (fn)neN be a sequence in C(0, 1) and (a)keN a

(3) Let (fn)neN be a sequence in C(0, 1) and (a)keN a sequence of positive numbers, such that the series E1 9k a converges and such that ISk+1 - Sell S ar for all keN. Show that Snta(@) - fn(z) S |fnsk - fall sEas jan for all n, k eN and z (0, 1). Use this to show that C((0, 1]) is complete.

Step by Step Solution

★★★★★

3.44 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Completeness of C01 with sup norm assume that eo1 with st... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let (xn) and (yn) be sequences of positive numbers such that lim(xn/yn) = 0. (a) Show that if lim(xn) = +, then lim(yn) = + . (b) Show that if (yn) is bounded, then lim(xn) = 0.

Let (xn) and (yn) be sequences of positive numbers such that lim(xn/yn) = + , (a) Show that if lim(yn) = + , then lim(xn) = + . (b) Show that if (xn) is bounded, then lim(yn) = 0.

Let {bn} a sequence of positive numbers that converges to 1/2. Determine whether the given series is absolutely convergent. ba cos m

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Comparative Programming Languages.Make sense of what certified influence all of the three terms is endeavoring to show and get a handle on what all of the going with pictures suggests, inside the...

) Consider integer division of one two's-complement binary number by another. Programming languages may vary in the result when one argument is negative. What differing conventions might they be...

You are designing a new syntax for a programming language like Java, with the intention of making it more approachable to students by using English words instead of punctuation symbols. (a) How does...

Discrete Math Fall 2017 Homework 7 Due: Friday, November 10, 2017 The below problems involve material from Chapter 5. You must type your solutions. Submit a single PDF file on eLC by 9PM on the given...

0, 05151/ n, (a) un (I) = n, 1 0 be a fixed real number, and define |ul = sup(|(x)| : (x| s a} and | |ull| = min(1, Ilu][) on the space C(-co, co). Why is || - || not a norm? Is ||| - ||| a norm?...

References: Health Information Management Case Studies Second Edition AHIMA by Dianna M. Foley Health Information Management Technology an Applied Approah Sixth Edition AHIMA by Nanette Sayles and...

Describe the process for selling to foreign governments and state enterprises.

Step 1: Select one of the following IT infrastructure components: Computer hardware platforms Operating system platforms Enterprise software applications Data management and storage . ...

For the convergent alternating series k = 0 ( - 1 ) k ( 2 k + 3 ) ! , evaluate the n t h partial sum for n = 3 . Then find a n upper bound for the error | S - S n | i n using the n t h partial sum S...

Identify and briefly compare the two leading stock exchanges in the United States today.

Indicate whether the following instruments are examples of money market or capital market securities. a. U.S. Treasury bills b. Long-term corporate bonds c. Common stocks d. Preferred stocks e....

A woman went to the Beneficial Loan Company and borrowed $3000. She must pay $119.67 at the end of each month for the next 30 months. (a) Calculate the nominal annual interest rate she is paying to...

If, in Example 4, one molecule of the product C is formed from one molecule of the reactant A and one molecule of the reactant B, and the initial concentrations of A and B have a common value [A] =...

Block a in Fig. 5.69 has a mass of 4.00 kg, and block B has mass 12.0 kg. The coefficient of kinetic friction between block B and the horizontal surface is 0.25. (a) What is the mass of block C if...

Isye Question 1 1 pts Which statement correctly describes the conditional variance structure in the ARCH model? O The variance depends on the future data points only. The variance remains strictly...

Problem 3. Let f(n) be a function of positive integer n. We know: We know: f(1)=f(2)==f(1000)=1 and for n>1000 f(n)=5n+f(n/1.01). Prove f(n)=O(n). Recall that x is the ceiling operator that returns...

Let B be a subset of Nm, m > 1. We say that B is r.e. if B = {(x1 , ... , xm) E Nm I g(xto ... , xm)H for some partially computable function g(x1 , ??? , xm). Let Show that B' is r.e. if and only if...

Can someone please show me how I would go about doing these? Thanks. For each assertion in 7(a)-(c), prove the assertion directly from the definition of the big-O asymptotic notation if it is true by...

SAMPLING MEAN: DEFINITION: The term sampling mean is a statistical term used to describe the properties of statistical distributions. In statistical terms, the sample mean from a group of...

I want the answer of below question of financial mathematics 7:15 PM Sun 15 Nov Homework 2 (1 of 6) 3. Let p E (0, 1). Consider (Xi),-21 i.i.d., where each X,- = 1 with probability p, and = 1 with...

1 Let (an) nen be a sequence. (a) Prove that if lim an = L exists, then every subsequence of (an)ner tends to L. 1-+0o (b) Prove that if every subsequence of (an )nel is convergent, then (an)EN is...