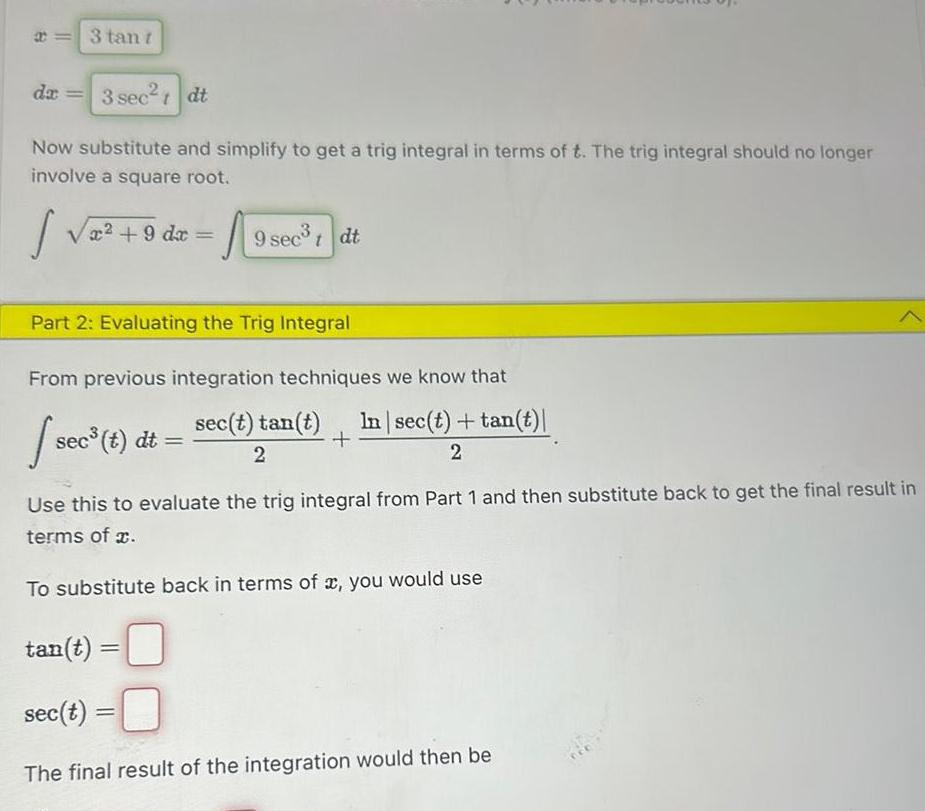
3 tant dx=3 sect dt Now substitute and simplify to get a trig integral in terms of t. The trig integral should no longer involve a square root. x+9 dx= 9 sect dt Part 2: Evaluating the Trig Integral From previous integration techniques we know that [sec (t) dt = sec(t) tan(t) In sec(t)+tan(t)] + 2 2 Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of x. To substitute back in terms of x, you would use tan(t)= = sec(t)=0 The final result of the integration would then be