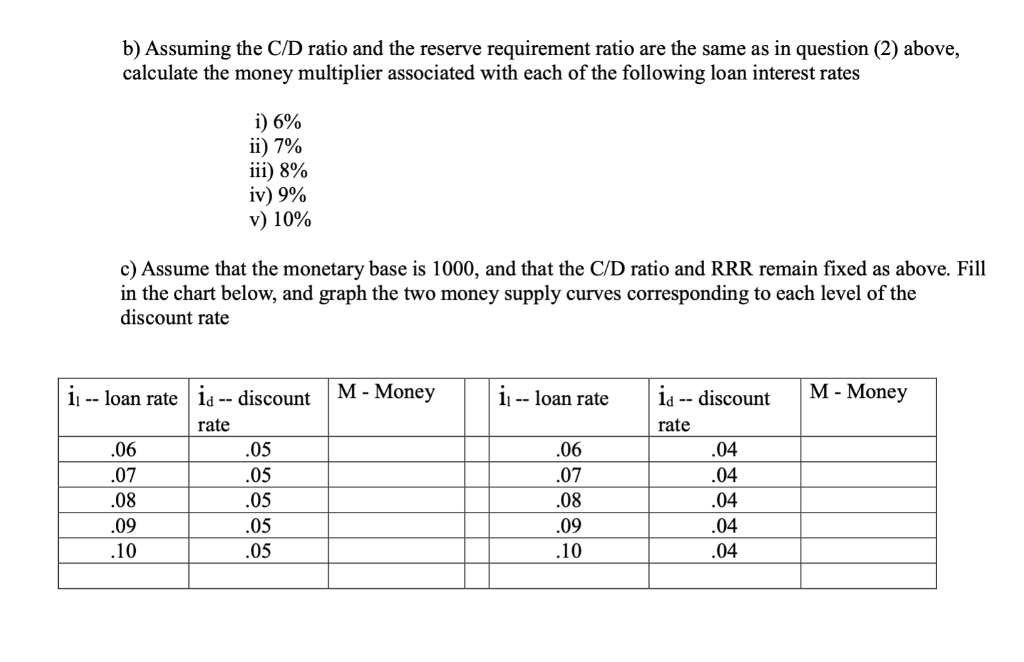
3. The cost to banks of accidentally being caught short of reserves is equal to the rate charged by the Fed on discount loans. The higher a banks excess reserves, the lower its likely need for borrowing. The benefit to a bank of keeping excess reserves small is that it earns interest on more loans. Thus, it makes sense to claim that the excess-reserves-to-deposits ratio depends on the difference between the loan rate of interest and the discount rate. Of course this ratio must lie in the (0,1) interval. Assume that the specific functional form is the following: ER 1 1+ exp[100 * (12-22 (This is a sigmoid function which maps the difference between loan and discount rates of interest onto the bounded (0,1) interval. As the difference goes to infinity, the function approaches 0; as the difference goes to negative infinity, the function approaches 1). a) Assume the discount rate is 5% (.05). Calculate the ER/D ratio for values of the loan rate of interest of i) 6% ii) 7% iii) 8% iv) 9% v) 10% b) Assuming the C/D ratio and the reserve requirement ratio are the same as in question (2) above, calculate the money multiplier associated with each of the following loan interest rates i) 6% ii) 7% iii) 8% iv) 9% v) 10% c) Assume that the monetary base is 1000, and that the C/D ratio and RRR remain fixed as above. Fill in the chart below, and graph the two money supply curves corresponding to each level of the discount rate ii -- loan rate id -- discount M - Money ii -- loan rate id -- discount M - Money rate rate .06 .07 .08 .09 .10 .05 .05 .05 .05 .05 .06 .07 .08 .09 .10 .04 .04 .04 .04 .04 3. The cost to banks of accidentally being caught short of reserves is equal to the rate charged by the Fed on discount loans. The higher a banks excess reserves, the lower its likely need for borrowing. The benefit to a bank of keeping excess reserves small is that it earns interest on more loans. Thus, it makes sense to claim that the excess-reserves-to-deposits ratio depends on the difference between the loan rate of interest and the discount rate. Of course this ratio must lie in the (0,1) interval. Assume that the specific functional form is the following: ER 1 1+ exp[100 * (12-22 (This is a sigmoid function which maps the difference between loan and discount rates of interest onto the bounded (0,1) interval. As the difference goes to infinity, the function approaches 0; as the difference goes to negative infinity, the function approaches 1). a) Assume the discount rate is 5% (.05). Calculate the ER/D ratio for values of the loan rate of interest of i) 6% ii) 7% iii) 8% iv) 9% v) 10% b) Assuming the C/D ratio and the reserve requirement ratio are the same as in question (2) above, calculate the money multiplier associated with each of the following loan interest rates i) 6% ii) 7% iii) 8% iv) 9% v) 10% c) Assume that the monetary base is 1000, and that the C/D ratio and RRR remain fixed as above. Fill in the chart below, and graph the two money supply curves corresponding to each level of the discount rate ii -- loan rate id -- discount M - Money ii -- loan rate id -- discount M - Money rate rate .06 .07 .08 .09 .10 .05 .05 .05 .05 .05 .06 .07 .08 .09 .10 .04 .04 .04 .04 .04