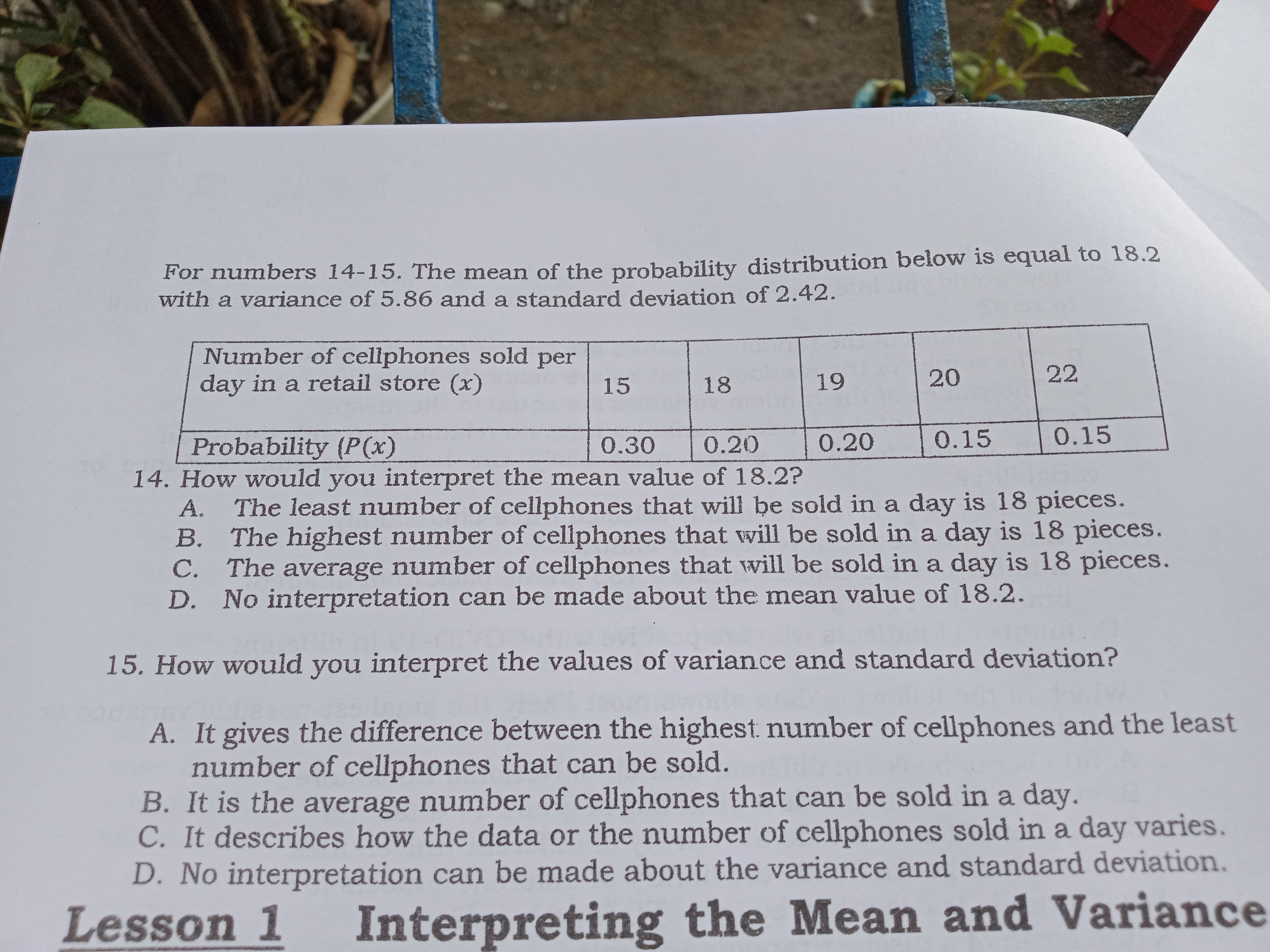
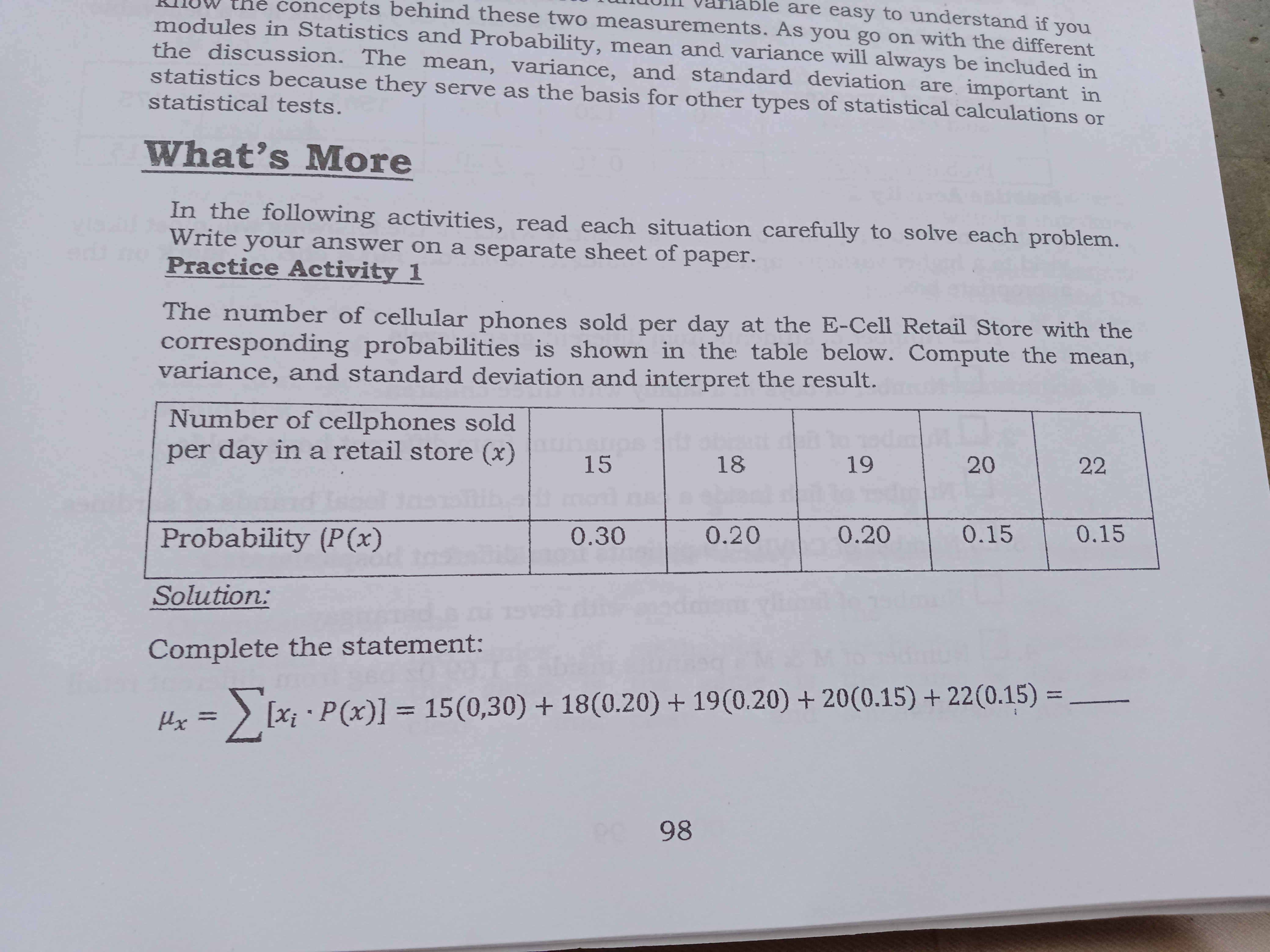
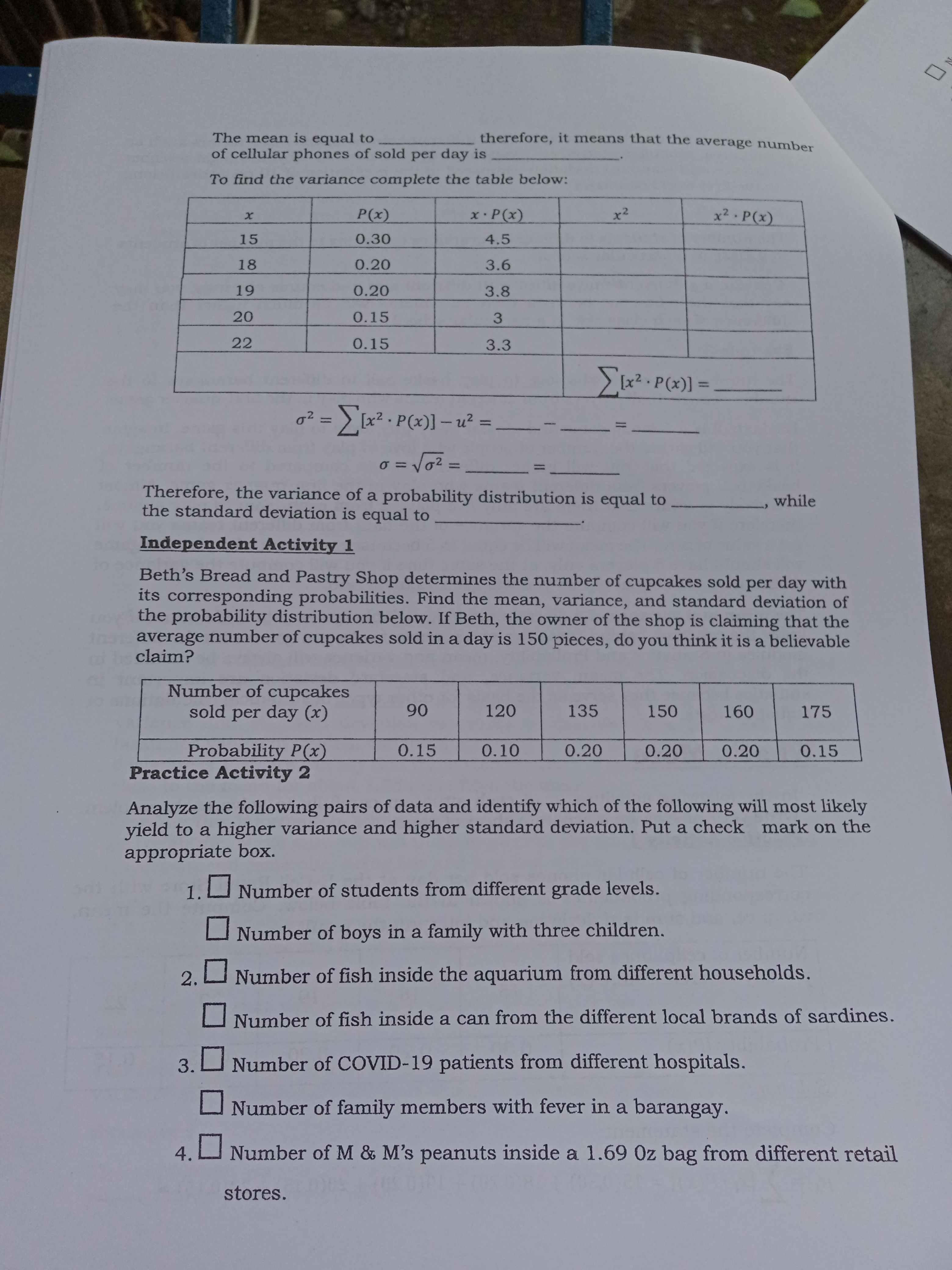
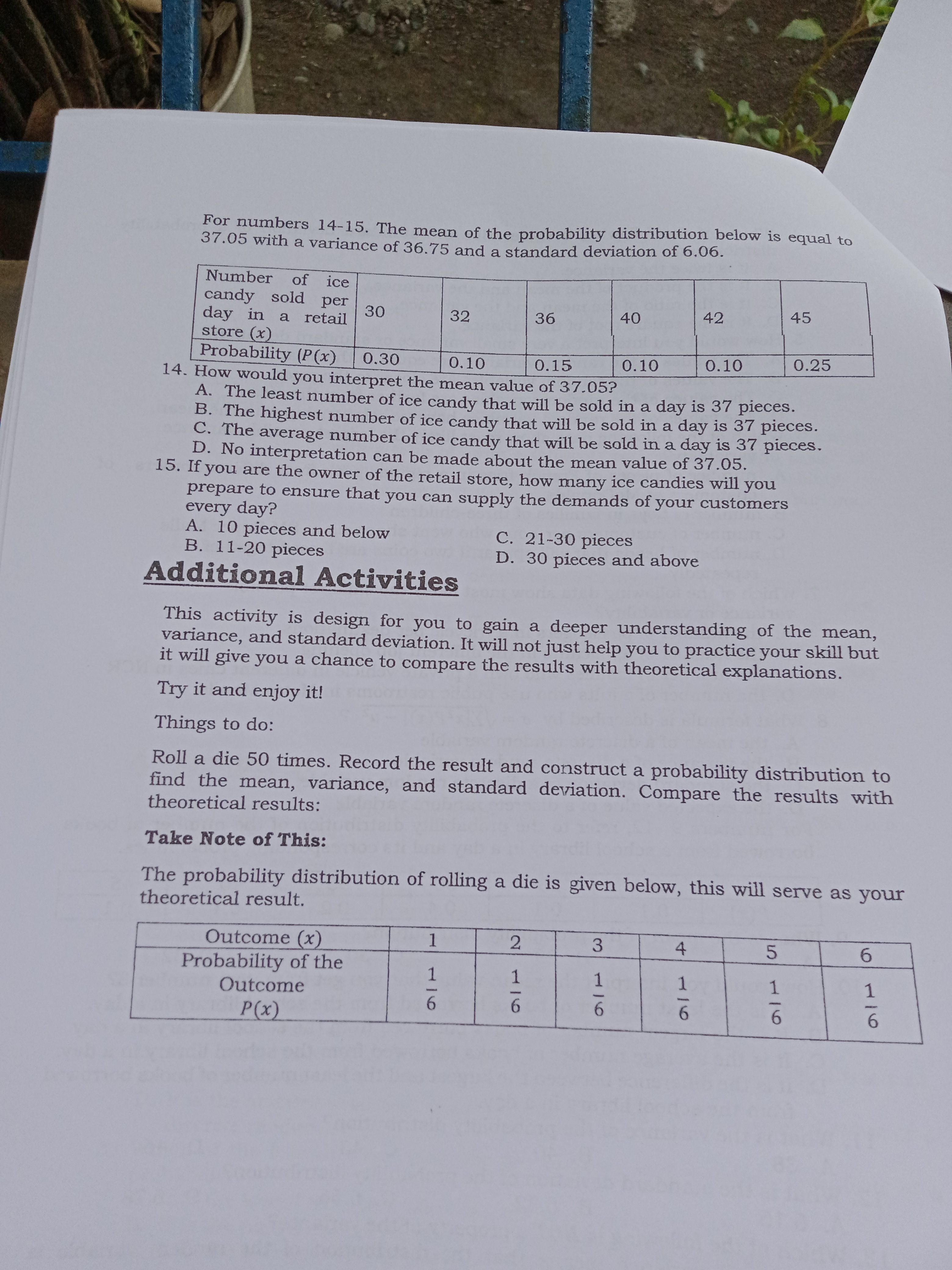
3 What I Need to Know This module was designed and written with you in mind. It is here to help you understand why we need to find the mean and variance of a discrete random variable and how to interpret it. The language used recognizes the diverse vocabulary level of students. The lessons are arranged to follow the standard sequence of the course But the order in which you read them can be changed to correspond with the textbook you are now using. This module has only one lesson which focuses on interpreting the mean and variance of a discrete random variable. Your knowledge and skill on how to use the formula for the mean, variance, and standard deviation that you learned from previous modules are pre-requisite skills. Accurate computations will yield accurate interpretations. In case that there will be mistakes in the calculations of mean, variance, and standard deviation, interpretation of the data will be affected, And if we interpret the result based on the miscalculations, our tendency to make a not so wise decision is higher. So, to be successful in this module, always review your computations before you make interpretations. Expect also that some of the practice exercises and problems included here need your patience and determination because it requires long computations. It will teach you the virtues of being patient and striving for excellence. Bear in mind that you need to review first your solutions to arrive with accurate interpretations. So, are you now ready? Let us start your journey today. After going through this module, you are expected to: 1. interpret the mean and variance of a discrete random variable; and 2. recall and apply the formulas for the mean, variance, and standard deviation of a discrete random variable. What I Know Before studying this module, take this test to determine what you already know about the topic covered. Choose the letter of the best answer. Write the chosen letter on a separate sheet of paper. 1. What do you call a random variable with possible values that form a finite or countable set? A. continuous C. finite B. discrete D. infinite 2. What term is used to describe the average value of a discrete random variable over numerous trials of an experiment? A. mean C. standard deviation B. probability D. variance 3. Which of the following represents the amount of spread, dispersion, or variability of the items in a distribution? A. mean or expected value B. median and mode C. outcomes and probability distribution D. variance and standard deviation 4. Which of the following is also equal to the square root of the variance? A. mean C. probability 93e to help you variable JO To B. median (D. standard deviation to zero? 5. How would you interpret a very small variance or standard deviation but not equal A. The values of the random variables are farther from the mean. B. The values of the random variables are nearer to the mean. C. The values of the random variables are equal to the mean. D. The values of the random variables have no relationship with the mean. variability? 6. Which of the following shows most likely the largest possible variance or A. number of girls in a randomly selected three-child family B. number of newborn babies per minute. C. number of Oreo cookies inside a 133 grams pack from different branch of 711 stores D. number of patients who are positive with COVID-19 in different hospitals 7. Which of the following data shows most likely the smallest possible variance or variability? A. number of books in different branch of National Bookstore B. number of books inside a pack bag of grade 11 students C. number of books inside the library of different universities D. number of books inside the library of different households 8. What formula is described by o = E[x2P(x)]--uz? A. the mean of a discrete random variable B. the variance of a discrete random variable C. the standard deviation of a discrete random variable D. the expected value of a discrete random variable For numbers 9-12, refer to the probability distribution of rolling a single unfair die. X 2 3 4 5 6 P(x ) 0.1 0. 1 0. 1 0.5 0.1 0 . 1 9. What is the mean of the probability distribution? A. 2.5 B. 3.7 C. 4.1 D. 5.7 10. What is the variance of the probability distribution? A. 1.81 B. 2.34 C. 3.70 D. 4.26 1 1. What is the standard deviation of the probability distribution? A. 1.07 B. 1.35 C. 1.92 D. 2.06 12. How would you interpret the mean value that you get in item number 9? A. The mean value is the difference between each probable value of the outcome when you roll the unfair die in numerous trials. B. The mean value is the higher probable value of the outcome when you roll the unfair die in numerous trials. C. The mean value is the lowest probable value of the outcome when you roll the unfair die in numerous trials. D. The mean value is the closest value to the most probable value of the outcome when you roll the unfair die in numerous trials. 13. Which of the following is NOT a property of the variance? A. The variance is not equal to the standard deviation. B. A small variance means that the distribution of the random variable is narrowly concentrated around the mean. C. A large variance means that the distribution is spread out, with some chance of observing values at some distance from the mean. D. The value of the variance is less than zero. 94For numbers 14-15. The mean of the probability distribution below is equal to 18.2 with a variance of 5.86 and a standard deviation of 2.42. Number of cellphones sold per day in a retail store (x) 15 18 19 20 22 Probability (P(x) 0.30 0.20 0.20 0.15 0.15 14. How would you interpret the mean value of 18.2? A. The least number of cellphones that will be sold in a day is 18 pieces. B. The highest number of cellphones that will be sold in a day is 18 pieces. C. The average number of cellphones that will be sold in a day is 18 pieces. D. No interpretation can be made about the mean value of 18.2. 15. How would you interpret the values of variance and standard deviation? A. It gives the difference between the highest number of cellphones and the least number of cellphones that can be sold. B. It is the average number of cellphones that can be sold in a day. C. It describes how the data or the number of cellphones sold in a day varies. D. No interpretation can be made about the variance and standard deviation. Lesson 1 Interpreting the Mean and Variancelable are easy to understand if you the concepts behind these two measurements. As you go on with the different modules in Statistics and Probability, mean and variance will always be included in the discussion. The mean, variance, and standard deviation are important in statistics because they serve as the basis for other types of statistical calculations or statistical tests. What's More In the following activities, read each situation carefully to solve each problem. Write your answer on a separate sheet of paper. Practice Activity 1 The number of cellular phones sold per day at the E-Cell Retail Store with the corresponding probabilities is shown in the table below. Compute the mean, variance, and standard deviation and interpret the result. Number of cellphones sold per day in a retail store (x) 15 18 19 20 22 Probability (P(x) 0.30 0.20 0.20 0.15 0.15 Solution: Complete the statement: Hx = ) [x; . P(x)] = 15(0,30) + 18(0.20) + 19(0.20) + 20(0.15) + 22(0.15) = _ 98The mean is equal to therefore, it means that the average number of cellular phones of sold per day is To find the variance complete the table below: x P (x ) x . P(x ) x 2 x 2 . P (x ) 15 0.30 4.5 18 0.20 3.6 19 0.20 3.8 20 0.15 3 22 0.15 3.3 [ [ x 2 . P( x )] = 8 2 = [ 1xx2. P ( )] - 12 = - - - ! = 0 = 102 = Therefore, the variance of a probability distribution is equal to the standard deviation is equal to , while Independent Activity 1 Beth's Bread and Pastry Shop determines the number of cupcakes sold per day with its corresponding probabilities. Find the mean, variance, and standard deviation of the probability distribution below. If Beth, the owner of the shop is claiming that the average number of cupcakes sold in a day is 150 pieces, do you think it is a believable claim? Number of cupcakes sold per day (x) 90 120 135 150 160 175 Probability P(x) 0.15 0.10 0.20 0.20 0.20 0.15 Practice Activity 2 Analyze the following pairs of data and identify which of the following will most likely yield to a higher variance and higher standard deviation. Put a check mark on the appropriate box. 1. Number of students from different grade levels. Number of boys in a family with three children. 2. Number of fish inside the aquarium from different households. Number of fish inside a can from the different local brands of sardines. 3. Number of COVID-19 patients from different hospitals. Number of family members with fever in a barangay. 4. Number of M & M's peanuts inside a 1.69 Oz bag from different retail stores.he average number Number of kernels in corn of different sizes. 5 . Number of players in a group playing the game "the boat is sinking." Number of passengers in different luxury cruise ships. Independent Activity 2 Give examples of at least two pairs of data that will most likely yield different variance and standard deviation. Identify the one with a higher possible value of variance and explain why. What I Have Learned Complete the following statements by writing the correct word or words. 1. The mean of a discrete random variable is interpreted as the value of a random variable over repeated trials of an experiment. 2. The variance and standard deviation of a discrete random variable measured or described the_ of the assumed values of the random variable to the mean. 3. A small variance or standard deviation means that the assumed values or data points tend to be to the mean. 4. A higher variance or standard deviation means that the assumed values or data points are from the mean What I Can doplay the game. details on how because how to play to play the audience cannot follow the game. game. the rules of the game. Assessment Multiple Choice. Choose the letter of the best answer. Write the chosen letter on a separate sheet of paper. 1. Which of the following is an example of a discrete random variable? A. weight of newborn babies B. body temperature of COVID-19 patients C. number of heads that will come out if you toss a coin twice D. height of basketball players 2. Which of the following best describe the mean of a discrete random variable? A. It is the lowest assumed value of a discrete random variable. B. It is the highest assumed value of a discrete random variable. C. It is the average value of a discrete random variable over numerous trials of an experiment. D. It is the amount of spread, dispersion, or variability of the assumed value of a discrete random variable. 3. Which of the following best describe the variance and standard deviation of a probability? A. It is the lowest assumed value of a discrete random variable. B. It is the highest assumed value of a discrete random variable. C. It is the average value of a discrete random variable over numerous trials of an experiment. D. It is the amount of spread, dispersion, or variability of the assumed value of a discrete random variable. 101distribution? . Which of the following best describe the standard deviation of a probability A. It is twice the variance. B. It is the product of the mean and the variance. C. It is the ratio of the mean and the variance. D. It is the square root of the variance. 5. How would you interpret a very small variance or standard deviation? A. The values of the random variables are equal to the mean. B. The values of the random variables are closer to the mean. C. The values of the random variables are farther from the mean. D. The values of the random variables have no relationship with the mean. 6. Which of the following data show most likely the largest possible variance or variability? A. number of pieces of French fries in a regular pack from different orders customers at Mcdonalds of B. number of boys in families of three-children C. number of customers per hour who went shopping at SM Super Malls repeatedly D. number of heads that will appear if two coins are tossed together 7. Which of the following data show most likely the smallest possible variance or variability? A. the number of passengers in a tricycle per destinations B. the number of applicants in the different job opening C. the number of families who own a private vehicle in different cities in NCR D. the number of adults who use public restrooms in Metro Manila 8. What formula is described by o = VE[x P(x)] -uz ? A. the mean of a discrete random variable B. the variance of a discrete random variable C. the standard deviation of a discrete random variable D. the expected value of a discrete random variable For numbers 9 -12, refer to the probability distribution of the number of books borrowed from a school library in a day and its corresponding probabilities. X 20 25 30 35 40 45 P(x ) 0. 1 0. 1 0.4 0.2 0. 1 0.1 9. What is the mean of the probability distribution? A. 25 B. 29 C. 30 D. 32 10. How would you interpret the mean value that you get from item number 8? A. It is the least number of books borrowed from the school library in a day. B. It is the largest number of books borrowed from the school library in a day. C. It is the average number of books borrowed from the school library in a day. D. It is the difference between the largest and the least number of books borrowed from the school library in a day. 11. What is the variance of the probability distribution? A. 38 B. 40 C. 43 D. 46 12. What is the standard deviation of the probability distribution? A. 6.16 B. 6.32 C. 6.56 D. 6.78 13. Which of the following is NOT a property of the variance? A. A small variance means that the distribution of the random variable is narrowly concentrated around the mean. B. A large variance means that the distribution is spread out, with some chance of observing values at some distance from the mean. C. The variance is a value that is always positive. D. The variance is a value that is always negative.For numbers 14-15. The mean of the probability distribution below is equal to 37.05 with a variance of 36.75 and a standard deviation of 6.06. Number of ice candy sold per day in a retail 30 32 36 40 42 45 store (x) Probability (P(x) 0.30 0.10 0.15 0.10 0.10 0.25 14. How would you interpret the mean value of 37.05? A. The least number of ice candy that will be sold in a day is 37 pieces. B. The highest number of ice candy that will be sold in a day is 37 pieces. C. The average number of ice candy that will be sold in a day is 37 pieces. D. No interpretation can be made about the mean value of 37.05. 15. If you are the owner of the retail store, how many ice candies will you prepare to ensure that you can supply the demands of your customers every day? A. 10 pieces and below C. 21-30 pieces B. 11-20 pieces D. 30 pieces and above Additional Activities This activity is design for you to gain a deeper understanding of the mean, variance, and standard deviation. It will not just help you to practice your skill but it will give you a chance to compare the results with theoretical explanations. Try it and enjoy it! Things to do: Roll a die 50 times. Record the result and construct a probability distribution to find the mean, variance, and standard deviation. Compare the results with theoretical results: Take Note of This: The probability distribution of rolling a die is given below, this will serve as your theoretical result. Outcome (x) 1 IN 3 4 6 Probability of the Outcome P(x)