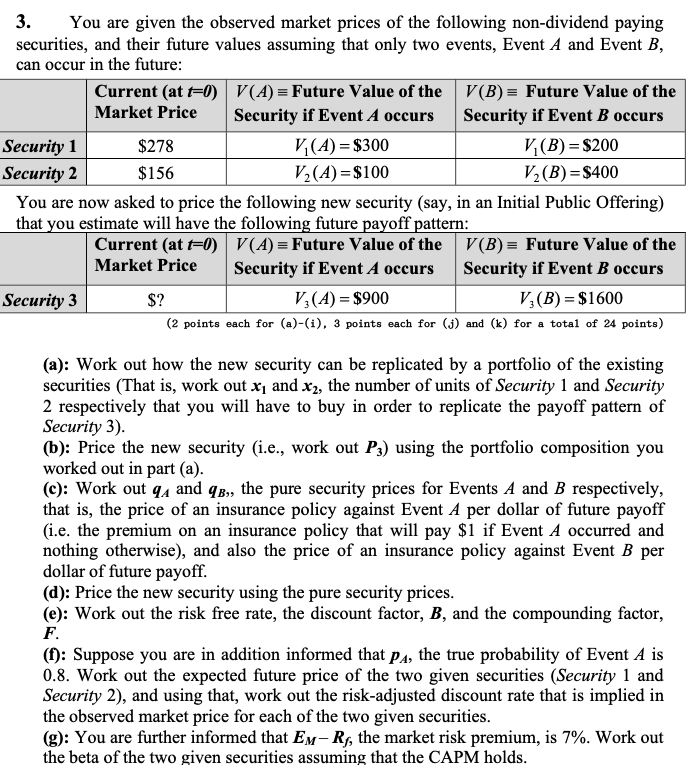
3. You are given the observed market prices of the following non-dividend paying securities, and their future values assuming that only two events, Event A and Event B, can occur in the future: Current (at 40) V(A) = Future Value of the V(B)= Future Value of the Market Price Security if Event A occurs Security if Event B occurs Security 1 $278 V(A) = $300 V(B) = $200 Security 2 $156 V2(A) = $100 V2(B) =$400 You are now asked to price the following new security (say, in an Initial Public Offering) that you estimate will have the following future payoff pattern: Current (at E0) V(A) = Future Value of the V(B) = Future Value of the Market Price Security if Event A occurs Security if Event B occurs Security 3 $? V (A) = $900 V (B) = $1600 (2 points each for (a)-(i), 3 points each for (j) and (k) for a total of 24 points) (a): Work out how the new security can be replicated by a portfolio of the existing securities (That is, work out x and X2, the number of units of Security 1 and Security 2 respectively that you will have to buy in order to replicate the payoff pattern of Security 3). (b): Price the new security (i.e., work out P3) using the portfolio composition you worked out in part (a). (c): Work out 94 and 9B,, the pure security prices for Events A and B respectively, that is, the price of an insurance policy against Event A per dollar of future payoff (i.e. the premium on an insurance policy that will pay $1 if Event A occurred and nothing otherwise), and also the price of an insurance policy against Event B per dollar of future payoff. (d): Price the new security using the pure security prices. (e): Work out the risk free rate, the discount factor, B, and the compounding factor, F. (f): Suppose you are in addition informed that Pa, the true probability of Event A is 0.8. Work out the expected future price of the two given securities (Security 1 and Security 2), and using that, work out the risk-adjusted discount rate that is implied in the observed market price for each of the two given securities. (g): You are further informed that Ex-Rs, the market risk premium, is 7%. Work out the beta of the two given securities assuming that the CAPM holds. 3. You are given the observed market prices of the following non-dividend paying securities, and their future values assuming that only two events, Event A and Event B, can occur in the future: Current (at 40) V(A) = Future Value of the V(B)= Future Value of the Market Price Security if Event A occurs Security if Event B occurs Security 1 $278 V(A) = $300 V(B) = $200 Security 2 $156 V2(A) = $100 V2(B) =$400 You are now asked to price the following new security (say, in an Initial Public Offering) that you estimate will have the following future payoff pattern: Current (at E0) V(A) = Future Value of the V(B) = Future Value of the Market Price Security if Event A occurs Security if Event B occurs Security 3 $? V (A) = $900 V (B) = $1600 (2 points each for (a)-(i), 3 points each for (j) and (k) for a total of 24 points) (a): Work out how the new security can be replicated by a portfolio of the existing securities (That is, work out x and X2, the number of units of Security 1 and Security 2 respectively that you will have to buy in order to replicate the payoff pattern of Security 3). (b): Price the new security (i.e., work out P3) using the portfolio composition you worked out in part (a). (c): Work out 94 and 9B,, the pure security prices for Events A and B respectively, that is, the price of an insurance policy against Event A per dollar of future payoff (i.e. the premium on an insurance policy that will pay $1 if Event A occurred and nothing otherwise), and also the price of an insurance policy against Event B per dollar of future payoff. (d): Price the new security using the pure security prices. (e): Work out the risk free rate, the discount factor, B, and the compounding factor, F. (f): Suppose you are in addition informed that Pa, the true probability of Event A is 0.8. Work out the expected future price of the two given securities (Security 1 and Security 2), and using that, work out the risk-adjusted discount rate that is implied in the observed market price for each of the two given securities. (g): You are further informed that Ex-Rs, the market risk premium, is 7%. Work out the beta of the two given securities assuming that the CAPM holds