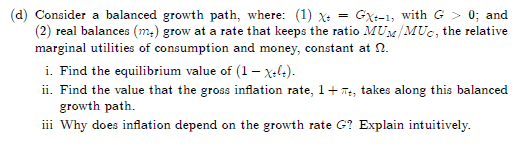

333Economics.
'f. Consider the following variant of the Lucas tree model. The preferences of the repre sentative consumer are E,(Z;3'1n[c.})_ s q: 3 q: 1, where :4 denotes consumption, and [-} denotes expectations conditional on time-t information. Output is produced by an innitelived tree: each period, the tree produces d, unite of non-storable output. Output is a non-negative, exogenous random variable governed by a Markov process with the stationary transition density.r f [11". d}. The economy starts o with each consumer owning one tree apiece. Let p, = pfcft} be the price at time t of all future prots from a tree, which we will call a unit of \"ideal stock". Let q{f.dt] be the kernel used to price the one-step- ahead contingent claim that delivers one unit of the consumption good when lit-HI. = If. Finally, let xi denote the consumer's nancial resources, which she allocates between ideal stock, contingent claims, and consumption. {a} 1li'ifrite down the consumer's problem in recursive form and nd the rst order conditions. [bi Show that the equilibrium price for ideal stock, it], can be written as as. {c} Now suppose that consumers have access to I"common stock'", which allows them to act as residual claimants. Each period a unit of common stock provides a dividend, 91., as follows: _ _ altdo. Essa Q'sHE''til{D lfdgsl'du ' Let at = o {it} be the price at time t to all future dividends from a unit of common stock. i. If an individual buys a unit of common stock in period t and sells it one period later, his income is the sum of the dividend 9H1 and the resale price 014.1. Combine this fact with the contingent claim price qfd'. dig} to derive an expression for a {sit}. ii. Impose the equilibrium allocation to derive an \"Euler equation\" for common stock. 3. Onesided search with multiple jobs Tirne: Discrete, innite horizon. Demography: Single worker who lives for ever. Preferences: The worker is riskneutral [i.e. rife} = :r} and discounts the future at the rate r. Ehrdcrwments: Regardless of how many jobs, i= D. l, 2... the worker currently has, with probability one. she receives an offer of another one. Every job pays the same wage, u: 2:: D l[no need for a distribution function]. 'With probability J'u. the worker looses a particular job. So if the worker has no job she gets Ill income. If she has 3 jobs she will earn inr. But because every job has the same chance of being destroyei when she has 11 jobs the probability that she will drop to having only i 1 jobs next period is 3.1.. {a} 1li'lr'rite down the ow value equations associated with each of: unemployment ll:i.e. Ii] jobs}, having 1 job and having 3' jobs [assume that all of the events are mutually exclusive and the probabilities are small enough that o. + L"; 3': l which works ne in continuous time}. {Use la: 1'1 and l",- for each value.) {b} I'l'ow dene 3'13,- = l; l;_1and solve for a dierence equation in in. [It should be a second order difference equation containing for example ll-+1. ,- and i_1.} {c} Show that there is a constant solution to the difference equation such that Q. = l- for all 3'. What is the value of if." {d} Now suppose there is a continuum [mass 1} of such workers. Draw the ow diagram associated with movements between each employment level. [As there are an innite set of employment levels the diagram has to only be indicative]I {e} 1W'rite down a rst order di'brenoe equation that can be used to solve for the steadystate numbers {masses} of workers in each state. Let nu. be the mass of unemployed: :11 be the mass of workers with '1 job and nl- be the mass of workers with ijobs. (Hint: the ow rate of people between having \"5 l and 3 jobs has to equal the rate at which people ow from i to 3' 1.} {f} Solve the di'erenoe equation forwards to obtain an expression for 33,- in terms of o. J... 3' and reg. {g} Imposing that E; 331- = 1 and using the general result that ll. Optimal Growth "with habit formation. Time: Discrete, innite horizon Dermgraphy: .-'-"L continuum, mass normalized to l, of {representative} innite lived eonsumer If" worker households. Preferences: The instantaneous household utility function over, current consumption, {2, and past eonsumption, c,_1. is nfq.c,_1}. The function n[.. .} is twice differentiable, strictly increasing in both arguments and and strictly concave. [The more you ate last period the more you like to eat this period] The discount factor is 3 E {I}. 1}. \"Technology: Each household has access to a neoclassical technology such that output per unit of labor is lo} where k: the capital stock owned by the household in period t and .) is twice differentiable, increasing and strictly concave. Households can eonvert the consumption good into capital one~forone. Capital depreciates through usage at the rate d. Endowments: Each households' initial capital stock is kn. Each household has 1 unit of time which it can devote in any proportions to labor or leisure. We are going to solve the Planner's problem recursively for this environment in two ways [the problems will actually diier very slightly} Approach 1: The rst approach uses in and ot_1 as the period t state variables. We need to assume that c_1 is given in this case. Approach 2: The second approach use! is} and Fct_1 as the period t state variables. We need to assume that 3L1 is given in this case. {a} For each approach: [It is ok to answer all three parts for I approach at a a time} i. write out the Planner's problem in recursive form. ii. Substitute 1::t out of each problem and obtain rst order conditions with re spect to foH. (Hint: for Approach 2 you will need to substitute out q_1 as well.) iii. 1W'rite out the envelope conditions and solve for an Euler equation. {b} Interpret the Euler equation that you have derived {they should both be the same}. {c} How does the interior steadysate, [c', k'} di'er from the standard model without habit formation\"? (d) Consider a balanced growth path, where: (1) x: = Gxt-1, with G > 0; and (2) real balances (m,) grow at a rate that keeps the ratio MUM/MUc, the relative marginal utilities of consumption and money, constant at ?. i. Find the equilibrium value of (1 - x+(+). ii. Find the value that the gross inflation rate, 1 + 7, takes along this balanced growth path. iii Why does inflation depend on the growth rate G? Explain intuitively.l. The government benets paid to unemployed U.S. workers have recently become 1H5 generous. Although this cut 'ilr'lll reduce the number of unemployed workers: it will not affect people already employed. 2. Increasing the tax rate on capital income will have very little effect on workers. as most workers own very fessr assets. 3. Ination is exclusively a monetary phenomenon 4-. As cashinadvance induces an indirect utility function over money. it is simply a special case of money in the utility function. 5. During the Great Recession MDTEND, unemployment roseJ because the natural rate of unemployment rose. The search and matching approach to labor markets explains why the natural rate rose. 6'. Real business cycle theory provides an explanation of how a malfunction of debt mar kets can reduce national income and product