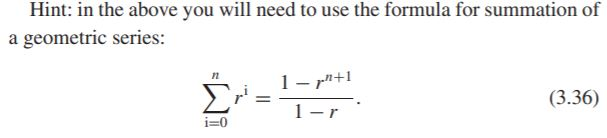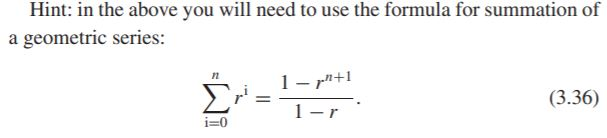
3.5 The continually branching circulatory system can be modeled as a branching network in which each junction contains a parent tube and two daughter tubes of equal diameter. This model can be used to give a rough estimate of pressure drop as a function of position within the arterial tree. Properties of the vessels in generation n (i.e., after n branchings) are designated by the subscript n. The aorta is considered to be generation zero. Assume that Poiseuille's law holds in each generation with a high shear) value for Meff of 3.5 CP. You may also assume that the length to diameter ratio Ln/D, is constant and equal to 16 in all generations (i.e., for all n). The bifurcations are characterized by the area ratio a, defined by a = area of daughter tubes area of parent tube (3.33) You may assume that a is the same for each generation. (a) Show that Dn = (a/2)/2D. (b) Show that Apn = Apo(2/a3yn/2, and hence that the total pressure drop from the root of the aorta to the end of the Nth generation pipe, Apo-N, [(2/3)N+1)/2-17 Apo-N = Apo L (2/a3)1/2 - 1 (3.34) (c) Show that the total volume of the system from the root of the aorta to the end of the Nth generation Vo-n, is 11 - (/2)(N+1)/27 Vo-N = V. (3.35) L1-Q3/2)/2 (d) The aortic volume V, is 100 ml, and the total volume Vis approximately 1200 ml. Use these facts to show that a = 1.189 when N is very large. (e) Our assumption of Poiseuille flow will break down in the smaller arteri- oles, when the diameter is approximately 20 um. Knowing that average aortic diameter is 2 cm, estimate the number of generations N up to which the formula in part (b) is valid. Make a table showing n, the total number of vessels in the nth generation; the length from the root of the aorta to the end of the nth generation; and the pressure at the beginning of the nth generation. Take Q = 5 l/min and assume a pressure at the aortic root of 100 mmHg. In your table, include values of n from zero (the aorta) to the number of generations which you found above, in steps of 3; i.e., you will have entries for n = 0, 3, 6, ... Hint: in the above you will need to use the formula for summation of a geometric series: x= (3.36) (3.36) 3.5 The continually branching circulatory system can be modeled as a branching network in which each junction contains a parent tube and two daughter tubes of equal diameter. This model can be used to give a rough estimate of pressure drop as a function of position within the arterial tree. Properties of the vessels in generation n (i.e., after n branchings) are designated by the subscript n. The aorta is considered to be generation zero. Assume that Poiseuille's law holds in each generation with a high shear) value for Meff of 3.5 CP. You may also assume that the length to diameter ratio Ln/D, is constant and equal to 16 in all generations (i.e., for all n). The bifurcations are characterized by the area ratio a, defined by a = area of daughter tubes area of parent tube (3.33) You may assume that a is the same for each generation. (a) Show that Dn = (a/2)/2D. (b) Show that Apn = Apo(2/a3yn/2, and hence that the total pressure drop from the root of the aorta to the end of the Nth generation pipe, Apo-N, [(2/3)N+1)/2-17 Apo-N = Apo L (2/a3)1/2 - 1 (3.34) (c) Show that the total volume of the system from the root of the aorta to the end of the Nth generation Vo-n, is 11 - (/2)(N+1)/27 Vo-N = V. (3.35) L1-Q3/2)/2 (d) The aortic volume V, is 100 ml, and the total volume Vis approximately 1200 ml. Use these facts to show that a = 1.189 when N is very large. (e) Our assumption of Poiseuille flow will break down in the smaller arteri- oles, when the diameter is approximately 20 um. Knowing that average aortic diameter is 2 cm, estimate the number of generations N up to which the formula in part (b) is valid. Make a table showing n, the total number of vessels in the nth generation; the length from the root of the aorta to the end of the nth generation; and the pressure at the beginning of the nth generation. Take Q = 5 l/min and assume a pressure at the aortic root of 100 mmHg. In your table, include values of n from zero (the aorta) to the number of generations which you found above, in steps of 3; i.e., you will have entries for n = 0, 3, 6, ... Hint: in the above you will need to use the formula for summation of a geometric series: x= (3.36) (3.36)