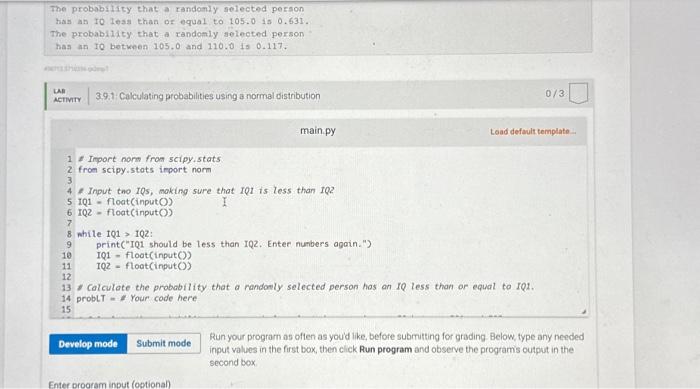
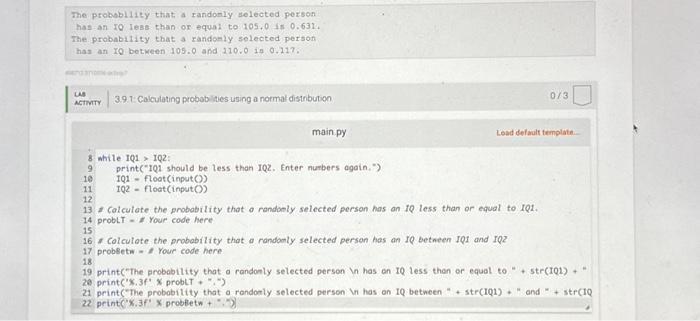
​​​​

3.9 LAB: Calculating probabilities using a normal distribution The intelligence quotient (IQ) of a randomly selected person follows a normal distribution with a mean of 100 and a standard deviation of 15. Use the scipy function norm and user input values for 101 and 102 to perform the following tasks Calculate the probability that a randomly selected person will have an IQ less than or equal to 101 Calculate the probability that a randomly selected person will have an IQ between 101 and 102 For example, if the input is 105 110 the output is The probability that a randomly selected person has an 10 less than or equal to 105.0 in 0.631. The probability that a randomly selected person has an 10 between 105.0 and 110.0 is 0.117. LAB ACTIVITY 3.9.1: Calculating probabilities using a normal distribution 0/3 The probability that a randomly selected person has an 10 less than or equal to 105.0 is 0.631. The probability that a randomly selected person has an IQ between 105.0 and 110.0 is 0.117. LAB ACTIVITY 3.9.1: Calculating probabilities using a normal distribution 1# Import norm from scipy.stats 2 from scipy.stats import norm 3 4# Input tno IQs, making sure that IQ1 is less than 102 I 5 101 float(input()) 6 102 float(input()) 7 8 while 101 102: 9 10 print("IQ1 should be less than IQ2. Enter numbers again.") 101 float(input()) 102 float(input()) main.py Develop mode 11 12 13 Calculate the probability that a randomly selected person has an IQ less than or equal to 101. 14 probLT# Your code here 15 Submit mode Enter program input (optional) 0/3 Load default template... Run your program as often as you'd like, before submitting for grading Below, type any needed input values in the first box, then click Run program and observe the program's output in the second box The probability that a randomly selected person has an IQ less than or equal to 105.0 is 0.631. The probability that a randomly selected person has an IQ between 105.0 and 110.0 is 0.117. WASTONG LAB ACTIVITY 3.9.1: Calculating probabilities using a normal distribution 8 while IQ1 102: 9 main py print("101 should be less than IQ2. Enter numbers again."). float(input()) float(input()) IQ1 102 10 11 12 13 Calculate the probability that a randomly selected person has an IQ less than or equal to 101. 14 probLT Your code here 15 16 Colculate the probability that a randomly selected person has an IQ between IQ1 and IQ2 17 probletw#Your code here 18 19 print("The probability that a randomly selected person has an IQ less than or equal to 20 print('%.3 % probLT".") str(101) 21 print("The probability that a randomly selected person has on IQ between 22 print("%.3f X probletw 0/3 Load default template..... str(101)* and str(IQ