4 (Cumulative) - Google Chrome ylab.pearson.com/Student/Player Test.aspx?testld=236920996¢erwin=yes calculus SP 2022 Mya Evans 05/14/22 10:50 PM Test: Test 4 (Cumulative)

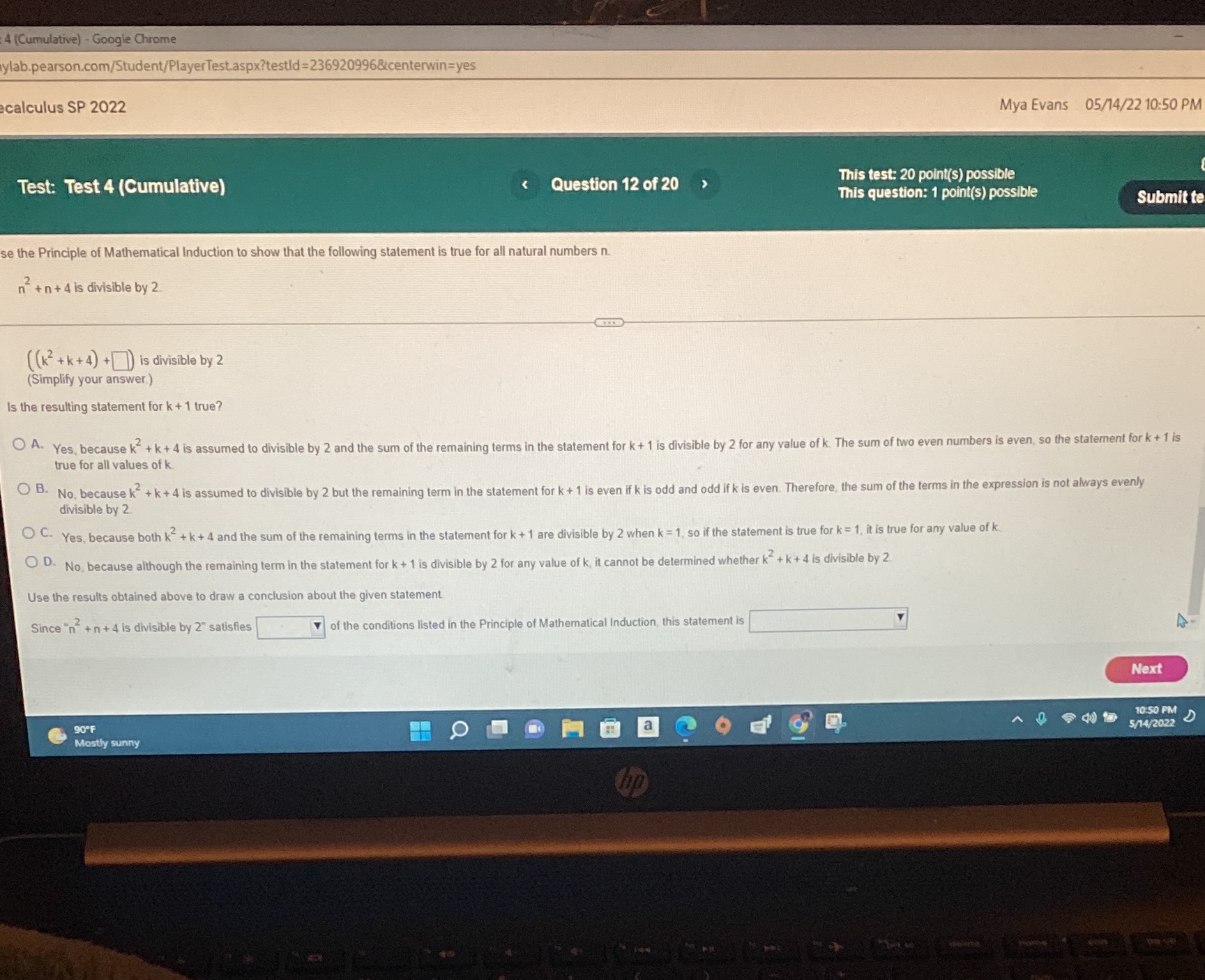
4 (Cumulatrve) - Goose Chrome 2calculus SP 2022 Test: Test 4 (Cumulative) Mya Evans 05/14/22 10:50 PM Question 12 of 20 This test: 20 point(s) ms question: 1 point(s) possible Submit te se the Principle of Mathematical Induction to show that the following statement is true for all natural numbers n. n + a is &visibIeby2 ((k2 + k +4) +0) is divisible by 2 (Simplify your answer ) Is the resulting statement for k + 1 true? O A' Yes, because k 4k +4 is assumed to divisible by 2 and the sum of the remaining terms in the statement for k+ 1 is divisible by 2 for any value of k The sum of two even numbers is even. so the statement fork + 1 is true for ail values ot k O B' No. because k + k +4 is assumed to divisible by 2 but the remaining term in the statement for k + 1 is even if k is odd and odd if k is evene Therefore, the sum of the terms in the expression is not always evenly divisible by 2 Yes. because both k + k +4 and the sum of the remaining terms in the statement for k +1 are divisible by 2 when k: 1, so if the statement is true for k: IL it is true for any value of k C) Noo because although the remaining term in the statement for 1 is divisible by 2 for any value of k, it cannot be determined whether k +k+4 is divisible by 2 Use the results obtained above to draw a conclusion about the given statement of the conditions listed in the Principle of Mathematical Inductionn this statement is Since -n + n +4 is divisible by 2" satisfies