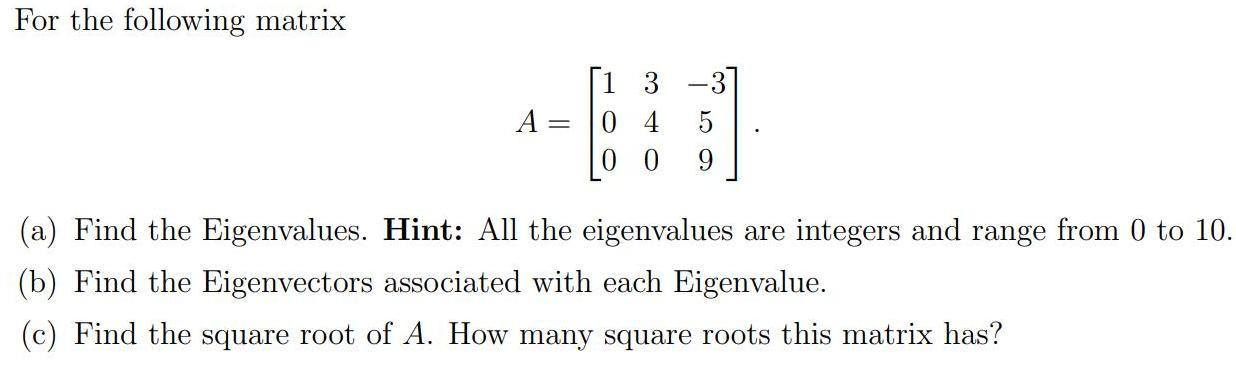
For the following matrix -3] 0 4 0 0 A = 5 9. (a) Find the Eigenvalues. Hint: All the eigenvalues are integers and range from 0 to 10. (b) Find the Eigenvectors associated with each Eigenvalue. (c) Find the square root of A. How many square roots this matrix has? Start from forming a new matrix by subtracting A from the diagonal entries of the given matrix: [1-X 3 -3 4 - X The determinant of the obtained matrix is - (A 9) (A 4) (A- 1) (for steps, see determinant calculator). Solve the equation - (A-9) (A- 4) (A 1) = 0. The roots are A1 = 9, A2 = 4, X3 = 1 (for steps, see equation solver). These are the eigenvalues. Next, find the eigenvectors. A= 9 1 - 3 -3 -8 -3 4 - X -5 9 - A The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. A = 4 [1-1 3 -3 -3 3 -3 4 - X 5 0 0 9 - A 5 The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. A = 1 TO 3 -31 0 3 [1-X 3 -3 4 - A 0 0 9 - A 0 0 8 The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. ANSWER Eigenvalue: 9 A, multiplicity: 1 A, eigenvector: 1 A. Eigenvalue: 4 A, multiplicity: 1 A, eigenvector: 1 A. Eigenvalue: 1 A, multiplicity: 1 A, eigenvector: 0 A. For the following matrix -3] 0 4 0 0 A = 5 9. (a) Find the Eigenvalues. Hint: All the eigenvalues are integers and range from 0 to 10. (b) Find the Eigenvectors associated with each Eigenvalue. (c) Find the square root of A. How many square roots this matrix has? Start from forming a new matrix by subtracting A from the diagonal entries of the given matrix: [1-X 3 -3 4 - X The determinant of the obtained matrix is - (A 9) (A 4) (A- 1) (for steps, see determinant calculator). Solve the equation - (A-9) (A- 4) (A 1) = 0. The roots are A1 = 9, A2 = 4, X3 = 1 (for steps, see equation solver). These are the eigenvalues. Next, find the eigenvectors. A= 9 1 - 3 -3 -8 -3 4 - X -5 9 - A The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. A = 4 [1-1 3 -3 -3 3 -3 4 - X 5 0 0 9 - A 5 The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. A = 1 TO 3 -31 0 3 [1-X 3 -3 4 - A 0 0 9 - A 0 0 8 The null space of this matrix is (for steps, see null space calculator). This is the eigenvector. ANSWER Eigenvalue: 9 A, multiplicity: 1 A, eigenvector: 1 A. Eigenvalue: 4 A, multiplicity: 1 A, eigenvector: 1 A. Eigenvalue: 1 A, multiplicity: 1 A, eigenvector: 0 A.