Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Let b > 0 and f : R R be defined by f(x) = 6. (a) If f'(0) exists, then (Fill in the blanks)
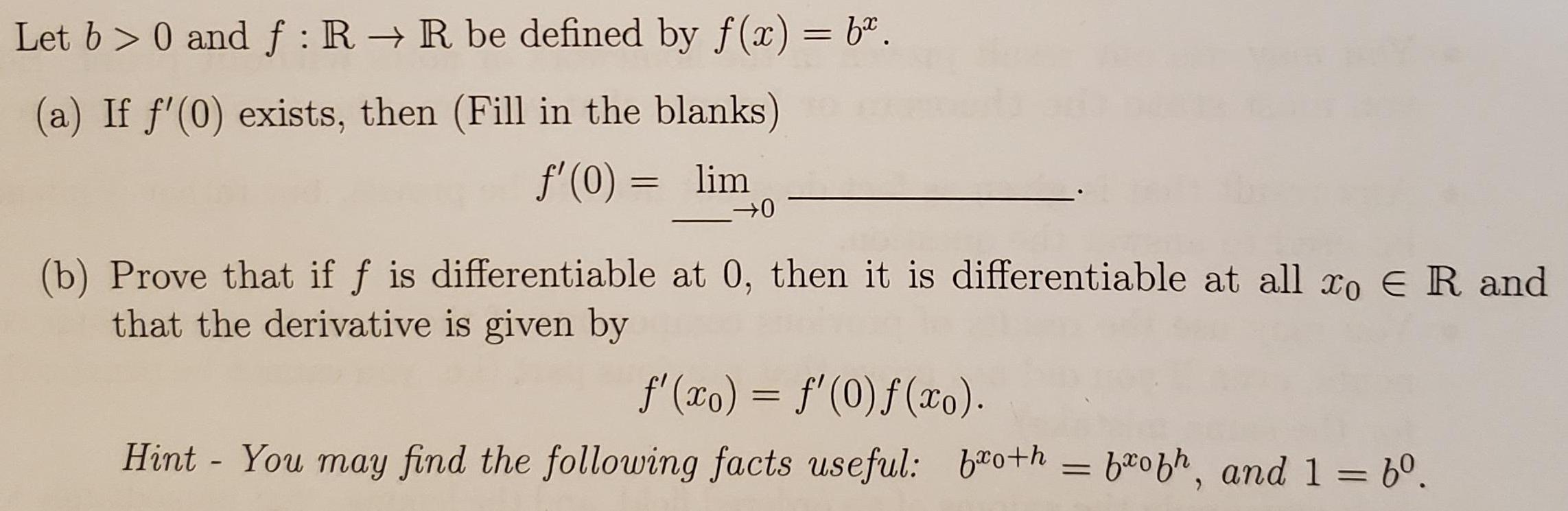
Let b > 0 and f : R R be defined by f(x) = 6". (a) If f'(0) exists, then (Fill in the blanks) f'(0) = lim (b) Prove that if f is differentiable at 0, then it is differentiable at all xo E R and that the derivative is given by f'(xo) = f'(0)f (xo). %3D Hint - You may find the follouwing facts useful: beoth = brobh, and 1 = 6. %3D
Step by Step Solution
There are 3 Steps involved in it
Step: 1
4Explanation 1 we have byo and IRIR be defined by fx b...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
An Introduction to the Mathematics of financial Derivatives
Authors: Salih N. Neftci
2nd Edition
978-0125153928, 9780080478647, 125153929, 978-0123846822
