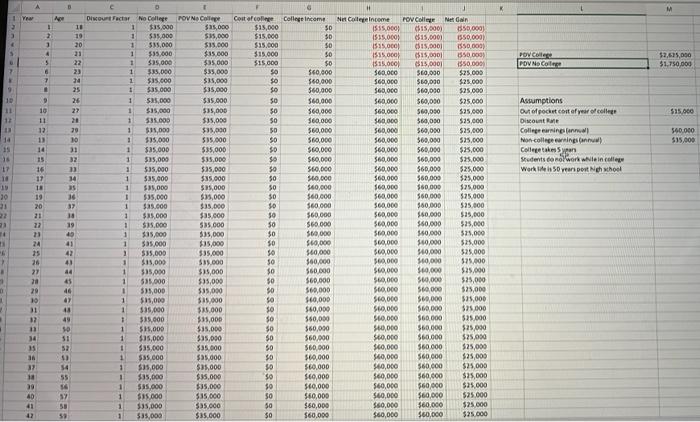
4. Suppose the cost of college doubles, to $30,000, without any changes in college income, non-college income, or discount rate.
a. What happens to the Internal Rate of Return, IRR? What is the new IRR?
b. What happens to the difference between PDV College and PDV No College
for a person with given discount rate?
c. If students differ by their personal discount rates, what would their discount
rate need to be to be just willing to go to college?
d. What would happen to the number of students deciding to go to college?
A D HI K M Year Ape College income 1 os 11 10 20 $0 2 3 4 5 1000'S POVN College $25,000 $35,000 $35.000 $15.000 $35 000 $35,00 $31.000 OS 01 Cost of conge $15,000 $15,000 $15.000 $15.000 $15.000 so $0 LE 5 $ 6000 1 22 23 POV College POV NO College $2.6.35,000 51.750.000 2 9 000 SES E 000'SES o os 9 10 25 26 27 $15.000 50 $0 50 $0 $0 12 11 14 $0 560.000 $60,000 560.000 $60,000 560,000 Se on 560,000 560,000 $60,000 $60,000 560.000 560.000 $15,000 ST 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Assumptions Out of pocket cost of year of college Discount College earnings Non-college caringan Collegetakeyan Students cool work while in cele work is 50 years post Ne hool 30 10 31 32 33 I COO'SES $35.000 $35,000 $35,000 $35.000 $35.000 $35,000 $35,000 $35,000 $35.000 $35,000 $35,000 $ $35.000 15 17 18 10 30 05 o$ o$ $0 000 ons DE SE os 50 TE 16 37 000 SES 000 SES Dior Factar No College 1 $35.000 1 $35.000 1 525.000 1 $35.000 1 $35.000 1 1 $35.000 1 $35.000 1 $35,000 1 $35,000 1 335.000 1 $11,000 1 $35.000 1 $35.000 1 1 $35.000 1 $35.000 1 $35,000 1 $35.000 1 1 $35.000 $15.000 1 $35,000 1 $35.000 1 $35,000 1 $15,000 1 $35,000 1 535.000 $35,000 1 $15,000 1 $35.000 1 $15.000 1 1 $35,000 1 $35.000 1 $35.000 1 $35,000 1 $35.000 1 1 $35.000 1 $35,000 1 $35,000 05 OS 22 23 14 $ Net Colincome POV College Net dan 1535.000 015,000) 350.000 1515.000 $15.0001 1550,000) 1515.000 550.000 1535.000 $15,000 1515.000 ($15,0001 $50.000 $60.000 $60,000 $25.000 560,000 $60,000 $25.000 $60,000 $60,000 $25.000 560.000 560,000 $25.000 560.000 569,000 $25.000 $60.000 560,000 $25.000 $60,000 569,000 $25.000 560.000 560,000 525.000 $60,000 560,000 $35.000 560.000 560,000 $35,000 560,000 560,000 $25,000 560.000 560.000 $25,000 $60,000 $60,000 $25.000 $60,000 560.000 525.000 $60,000 $60.000 525.000 $60,000 $50,000 $25,000 $60,000 $60,000 $25,000 560,000 550.000 525,000 $60,000 500,000 $25,000 $60,000 540,000 525.000 560.000 500,000 $75,000 S60,000 $69,000 $25.000 $60,000 S69,000 $25,000 560.000 560.000 $25,000 $60,000 $9,000 $25,000 560,000 $60,000 $25.000 $10,000 $60.000 525.000 $10,000 $60.000 $25,000 $10,000 $60.000 $25,000 $60,000 $60.000 $25,000 $40,000 $60,000 $25,000 $60,000 560.000 $25,000 $60,000 $60,000 $75,000 560,000 $60,000 $25.000 560,000 $60,000 $25.000 $50,000 $60.000 $25.000 $60,000 $60,000 $25.000 1 000 SES $40,000 $60.000 $60.000 $60,000 $60.000 $60,000 $60,000 360,000 $60,000 49 6 2 50 $0 50 $0 50 $0 $0 $0 50 24 25 26 27 28 29 10 31 000095 43 44 45 46 47 48 $35,000 $15,000 $35.000 $35.000 $35,000 $35,000 $35,000 $15,000 $35.000 $15,000 $35.000 1 1 os 20 I 13 es 000'51s 000'SCS $0 $0 $0 $0 PE SE WE 1 T 37 $60.000 $60,000 $60,000 $40,000 $60,000 $60,000 $60,000 $60,000 $60,000 $60,000 560,000 $60,000 560.000 $60,000 $60,000 54 33953SSES $35.000 $35.000 $35,000 $35,000 $35,000 BE 05 06 05 0$ OS 000 SES 6 57 000 SES 39 40 41 42 $35.000 $35,000 50 $0 Part 1: Human Capital Application: College education decision In class, we started with an appropriate discount rate that reflected our degree of patience and the rates of return on other investments. We then used that discount rate to calculate the present discounted value of the benefits minus the costs of a college degree. We said we should go to college if and only if that value were positive. There is another equivalent way of making the college decision in which we ask: how large can the discount rate be and still render the investment profitable? In practice, this means we (1) find the discount rate (r) that sets the costs equal to the benefits in present discounted value termswe call that discount rate the internal rate of return, and (2) go to college if the internal rate of return exceeds the return on other investments (our personal r). For example, if the internal rate of return is 4 percent and an equivalent investment in our next best investment opportunity (e.g., a mutual fund or business) offers a return of 5 percent (our r), we wouldn't go to college. Answer the following questions based on the Excel spreadsheet "Spreadsheet for extra credit," located in the Extra Credit directory of the Blackboard course website. Spend a few minutes familiarizing yourself with the sheet before you begin your work. Note the assumptions we begin with: Out of pocket cost of year of college $15,000 College earnings (annual): $60,000 Non-college earnings (annual): $35,000 College takes 5 years and students do not work while in college Work life is 50 years following high school Putting new numbers into the Assumptions in column M will automatically change the numbers in the calculations and the Present Discounted Values (PDV) for each year in Columns E and I, and in the sums in M5 and M6. Here are the questions: 2. What is the internal rate of return (approximated to the nearest hundredth, or better)? Use trial and error to find it. 3. Suppose in any high school graduate cohort, one third of graduates have a discount rate of 4 percent and two thirds have a discount rate of 9 percent. a. For the students graduating in a given year, what would be the average annual earnings by year (or age)? b. What would be the observed differences in Present Discounted Values at the time students graduated from high school? c. If all students had the same discount rate, equal to the internal rate of return, what would be the observed differences in Present Discounted Values at the time students graduated from high school? 4. Suppose the cost of college doubles, to $30,000, without any changes in college income, non-college income, or discount rate. a. What happens to the Internal Rate of Return, IRR? What is the new IRR? b. What happens to the difference between PDV College and PDV No College for a person with given discount rate? c. If students differ by their personal discount rates, what would their discount rate need to be to be just willing to go to college? d. What would happen to the number of students deciding to go to college? 5. Assume now that everyone's personal discount rate is the same. Further, assume that some persons decide to go to college, and some don't. a. What must be true about the internal rate of return (if we observe both college graduates and non-college graduates)? b. Inequality is sometimes measured by the annual earnings of the highest earners in the labor market compared to the annual earnings of the lowest earners. How much inequality is generated by the difference in incomes of individuals with and without college? c. Does the present discounted value (PDV) of wealth vary between college- educated and non-educated? d. How should we interpret the annual income differences? Does it reflect a lack of fairness or something else? e. Suppose the number of years of spent in college rose to six years (perhaps because of a rise in the educational requirements of jobs requiring a college degree). If discount rates do not change, what must happen to annual income differences? A D HI K M Year Ape College income 1 os 11 10 20 $0 2 3 4 5 1000'S POVN College $25,000 $35,000 $35.000 $15.000 $35 000 $35,00 $31.000 OS 01 Cost of conge $15,000 $15,000 $15.000 $15.000 $15.000 so $0 LE 5 $ 6000 1 22 23 POV College POV NO College $2.6.35,000 51.750.000 2 9 000 SES E 000'SES o os 9 10 25 26 27 $15.000 50 $0 50 $0 $0 12 11 14 $0 560.000 $60,000 560.000 $60,000 560,000 Se on 560,000 560,000 $60,000 $60,000 560.000 560.000 $15,000 ST 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Assumptions Out of pocket cost of year of college Discount College earnings Non-college caringan Collegetakeyan Students cool work while in cele work is 50 years post Ne hool 30 10 31 32 33 I COO'SES $35.000 $35,000 $35,000 $35.000 $35.000 $35,000 $35,000 $35,000 $35.000 $35,000 $35,000 $ $35.000 15 17 18 10 30 05 o$ o$ $0 000 ons DE SE os 50 TE 16 37 000 SES 000 SES Dior Factar No College 1 $35.000 1 $35.000 1 525.000 1 $35.000 1 $35.000 1 1 $35.000 1 $35.000 1 $35,000 1 $35,000 1 335.000 1 $11,000 1 $35.000 1 $35.000 1 1 $35.000 1 $35.000 1 $35,000 1 $35.000 1 1 $35.000 $15.000 1 $35,000 1 $35.000 1 $35,000 1 $15,000 1 $35,000 1 535.000 $35,000 1 $15,000 1 $35.000 1 $15.000 1 1 $35,000 1 $35.000 1 $35.000 1 $35,000 1 $35.000 1 1 $35.000 1 $35,000 1 $35,000 05 OS 22 23 14 $ Net Colincome POV College Net dan 1535.000 015,000) 350.000 1515.000 $15.0001 1550,000) 1515.000 550.000 1535.000 $15,000 1515.000 ($15,0001 $50.000 $60.000 $60,000 $25.000 560,000 $60,000 $25.000 $60,000 $60,000 $25.000 560.000 560,000 $25.000 560.000 569,000 $25.000 $60.000 560,000 $25.000 $60,000 569,000 $25.000 560.000 560,000 525.000 $60,000 560,000 $35.000 560.000 560,000 $35,000 560,000 560,000 $25,000 560.000 560.000 $25,000 $60,000 $60,000 $25.000 $60,000 560.000 525.000 $60,000 $60.000 525.000 $60,000 $50,000 $25,000 $60,000 $60,000 $25,000 560,000 550.000 525,000 $60,000 500,000 $25,000 $60,000 540,000 525.000 560.000 500,000 $75,000 S60,000 $69,000 $25.000 $60,000 S69,000 $25,000 560.000 560.000 $25,000 $60,000 $9,000 $25,000 560,000 $60,000 $25.000 $10,000 $60.000 525.000 $10,000 $60.000 $25,000 $10,000 $60.000 $25,000 $60,000 $60.000 $25,000 $40,000 $60,000 $25,000 $60,000 560.000 $25,000 $60,000 $60,000 $75,000 560,000 $60,000 $25.000 560,000 $60,000 $25.000 $50,000 $60.000 $25.000 $60,000 $60,000 $25.000 1 000 SES $40,000 $60.000 $60.000 $60,000 $60.000 $60,000 $60,000 360,000 $60,000 49 6 2 50 $0 50 $0 50 $0 $0 $0 50 24 25 26 27 28 29 10 31 000095 43 44 45 46 47 48 $35,000 $15,000 $35.000 $35.000 $35,000 $35,000 $35,000 $15,000 $35.000 $15,000 $35.000 1 1 os 20 I 13 es 000'51s 000'SCS $0 $0 $0 $0 PE SE WE 1 T 37 $60.000 $60,000 $60,000 $40,000 $60,000 $60,000 $60,000 $60,000 $60,000 $60,000 560,000 $60,000 560.000 $60,000 $60,000 54 33953SSES $35.000 $35.000 $35,000 $35,000 $35,000 BE 05 06 05 0$ OS 000 SES 6 57 000 SES 39 40 41 42 $35.000 $35,000 50 $0 Part 1: Human Capital Application: College education decision In class, we started with an appropriate discount rate that reflected our degree of patience and the rates of return on other investments. We then used that discount rate to calculate the present discounted value of the benefits minus the costs of a college degree. We said we should go to college if and only if that value were positive. There is another equivalent way of making the college decision in which we ask: how large can the discount rate be and still render the investment profitable? In practice, this means we (1) find the discount rate (r) that sets the costs equal to the benefits in present discounted value termswe call that discount rate the internal rate of return, and (2) go to college if the internal rate of return exceeds the return on other investments (our personal r). For example, if the internal rate of return is 4 percent and an equivalent investment in our next best investment opportunity (e.g., a mutual fund or business) offers a return of 5 percent (our r), we wouldn't go to college. Answer the following questions based on the Excel spreadsheet "Spreadsheet for extra credit," located in the Extra Credit directory of the Blackboard course website. Spend a few minutes familiarizing yourself with the sheet before you begin your work. Note the assumptions we begin with: Out of pocket cost of year of college $15,000 College earnings (annual): $60,000 Non-college earnings (annual): $35,000 College takes 5 years and students do not work while in college Work life is 50 years following high school Putting new numbers into the Assumptions in column M will automatically change the numbers in the calculations and the Present Discounted Values (PDV) for each year in Columns E and I, and in the sums in M5 and M6. Here are the questions: 2. What is the internal rate of return (approximated to the nearest hundredth, or better)? Use trial and error to find it. 3. Suppose in any high school graduate cohort, one third of graduates have a discount rate of 4 percent and two thirds have a discount rate of 9 percent. a. For the students graduating in a given year, what would be the average annual earnings by year (or age)? b. What would be the observed differences in Present Discounted Values at the time students graduated from high school? c. If all students had the same discount rate, equal to the internal rate of return, what would be the observed differences in Present Discounted Values at the time students graduated from high school? 4. Suppose the cost of college doubles, to $30,000, without any changes in college income, non-college income, or discount rate. a. What happens to the Internal Rate of Return, IRR? What is the new IRR? b. What happens to the difference between PDV College and PDV No College for a person with given discount rate? c. If students differ by their personal discount rates, what would their discount rate need to be to be just willing to go to college? d. What would happen to the number of students deciding to go to college? 5. Assume now that everyone's personal discount rate is the same. Further, assume that some persons decide to go to college, and some don't. a. What must be true about the internal rate of return (if we observe both college graduates and non-college graduates)? b. Inequality is sometimes measured by the annual earnings of the highest earners in the labor market compared to the annual earnings of the lowest earners. How much inequality is generated by the difference in incomes of individuals with and without college? c. Does the present discounted value (PDV) of wealth vary between college- educated and non-educated? d. How should we interpret the annual income differences? Does it reflect a lack of fairness or something else? e. Suppose the number of years of spent in college rose to six years (perhaps because of a rise in the educational requirements of jobs requiring a college degree). If discount rates do not change, what must happen to annual income differences