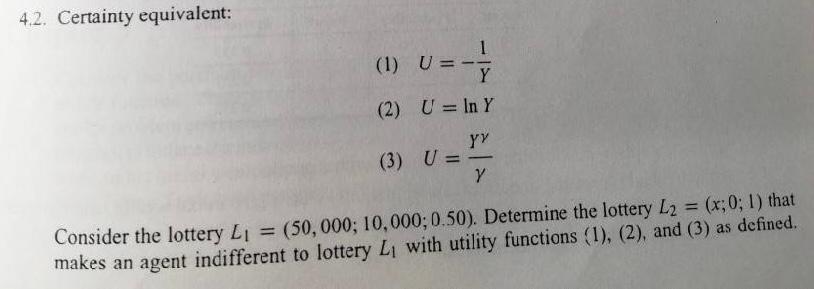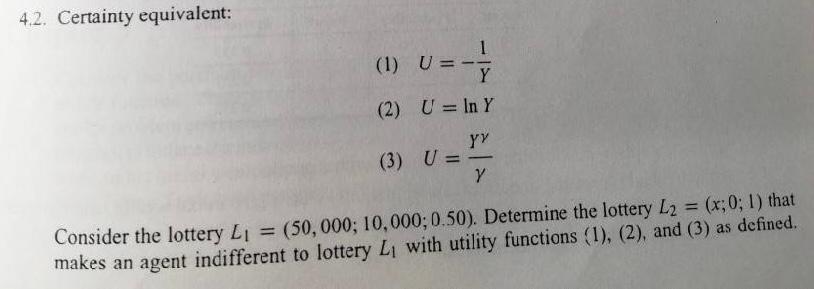

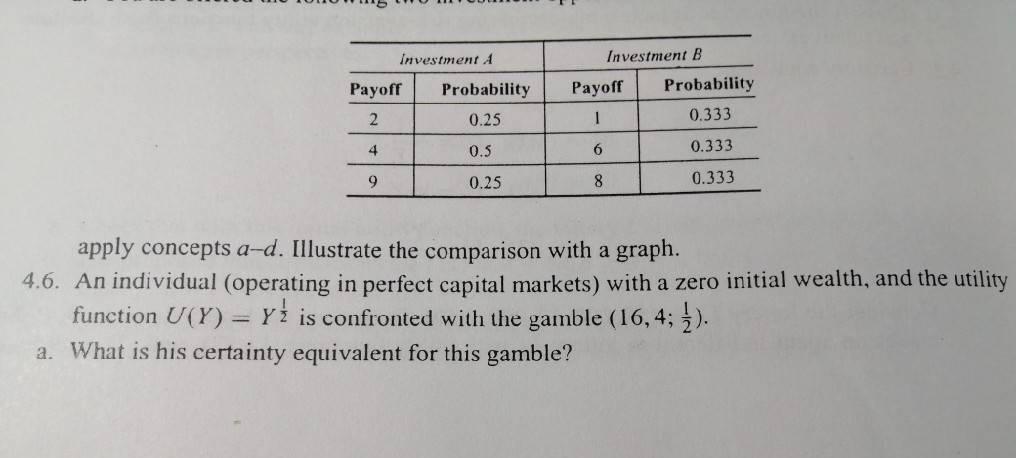

4.2. Certainty equivalent: (1) U= Y (2) U = In Y YY ) (3) U = Y Consider the lottery Li = (50,000; 10,000;0.50). Determine the lottery L2 = (x;0; 1) that makes an agent indifferent to lottery L, with utility functions (1), (2), and (3) as defined. For utility function (3), use y = {0.25,0.75). What is the effect of changing the value of y? Comment on your results using the notions of risk aversion and certainty equivalent. 4.3. Risk premium: A businesswoman runs a firm worth CHF 100,000. She faces some risk of having a fire that would reduce her net worth according to the following three states, i = 1,2,3, each with probability n(i) (Scenario A). State (i) Worth 1 0.01 2 0.04 50,000 3 0.95 100,000 Of course, in state 3, nothing detrimental happens, and her business retains its value of CHF 100,000 a. What is the maximum amount she will pay for insurance if she has a logarithmic utility function over final wealth? (Note: The insurance pays CHF 99,999 in the first case; CHF 50,000 in the second; and nothing in the third.) b. Do the calculations with the following alternative probabilities: Scenario B Scenario C (1) 0.01 0.02 (2) 0.05 0.04 TT (3) 0.94 0.94 Is the outcome the comparative change in the premium) a surprise? Why? Investment Investment B Payoff Payoff Probability Probability 0.25 2 1 0.333 4 0.5 6 0.333 9 0.25 8 0.333 apply concepts a-d. Illustrate the comparison with a graph. 4.6. An individual (operating in perfect capital markets) with a zero initial wealth, and the utility function U(Y) = y1 is confronted with the gamble (16,4; ). a. What is his certainty equivalent for this gamble? b. If there was an insurance policy that, together with the original gamble, would guarantee him the expected payoff of the gamble, what is the maximum premium he would be willing to pay for it? c. What is the minimum required increase the probability premium) in the probability of the high-payoff state so that he will not be willing to pay any premium for such an insurance policy? (Note that the insurance policy still pays the expected payoff of the unmodified gamble) d. Now assume that he is confronted with the gamble (36, 16; ). Calculate the certainty equiva- lent, the insurance premium, and the probability premium for this case as well. Explain what is going on, and why? 4.7. Refer to Table 3.2. Suppose the return data for investment 3 was as follows. Is it still the case Investment 3 Payoff Probability 3 0.25 4 0.5 12 0.25 that investment 3 SSD investment 4? Consider two investments with the following characteristics: 4.2. Certainty equivalent: (1) U= Y (2) U = In Y YY ) (3) U = Y Consider the lottery Li = (50,000; 10,000;0.50). Determine the lottery L2 = (x;0; 1) that makes an agent indifferent to lottery L, with utility functions (1), (2), and (3) as defined. For utility function (3), use y = {0.25,0.75). What is the effect of changing the value of y? Comment on your results using the notions of risk aversion and certainty equivalent. 4.3. Risk premium: A businesswoman runs a firm worth CHF 100,000. She faces some risk of having a fire that would reduce her net worth according to the following three states, i = 1,2,3, each with probability n(i) (Scenario A). State (i) Worth 1 0.01 2 0.04 50,000 3 0.95 100,000 Of course, in state 3, nothing detrimental happens, and her business retains its value of CHF 100,000 a. What is the maximum amount she will pay for insurance if she has a logarithmic utility function over final wealth? (Note: The insurance pays CHF 99,999 in the first case; CHF 50,000 in the second; and nothing in the third.) b. Do the calculations with the following alternative probabilities: Scenario B Scenario C (1) 0.01 0.02 (2) 0.05 0.04 TT (3) 0.94 0.94 Is the outcome the comparative change in the premium) a surprise? Why? Investment Investment B Payoff Payoff Probability Probability 0.25 2 1 0.333 4 0.5 6 0.333 9 0.25 8 0.333 apply concepts a-d. Illustrate the comparison with a graph. 4.6. An individual (operating in perfect capital markets) with a zero initial wealth, and the utility function U(Y) = y1 is confronted with the gamble (16,4; ). a. What is his certainty equivalent for this gamble? b. If there was an insurance policy that, together with the original gamble, would guarantee him the expected payoff of the gamble, what is the maximum premium he would be willing to pay for it? c. What is the minimum required increase the probability premium) in the probability of the high-payoff state so that he will not be willing to pay any premium for such an insurance policy? (Note that the insurance policy still pays the expected payoff of the unmodified gamble) d. Now assume that he is confronted with the gamble (36, 16; ). Calculate the certainty equiva- lent, the insurance premium, and the probability premium for this case as well. Explain what is going on, and why? 4.7. Refer to Table 3.2. Suppose the return data for investment 3 was as follows. Is it still the case Investment 3 Payoff Probability 3 0.25 4 0.5 12 0.25 that investment 3 SSD investment 4? Consider two investments with the following characteristics