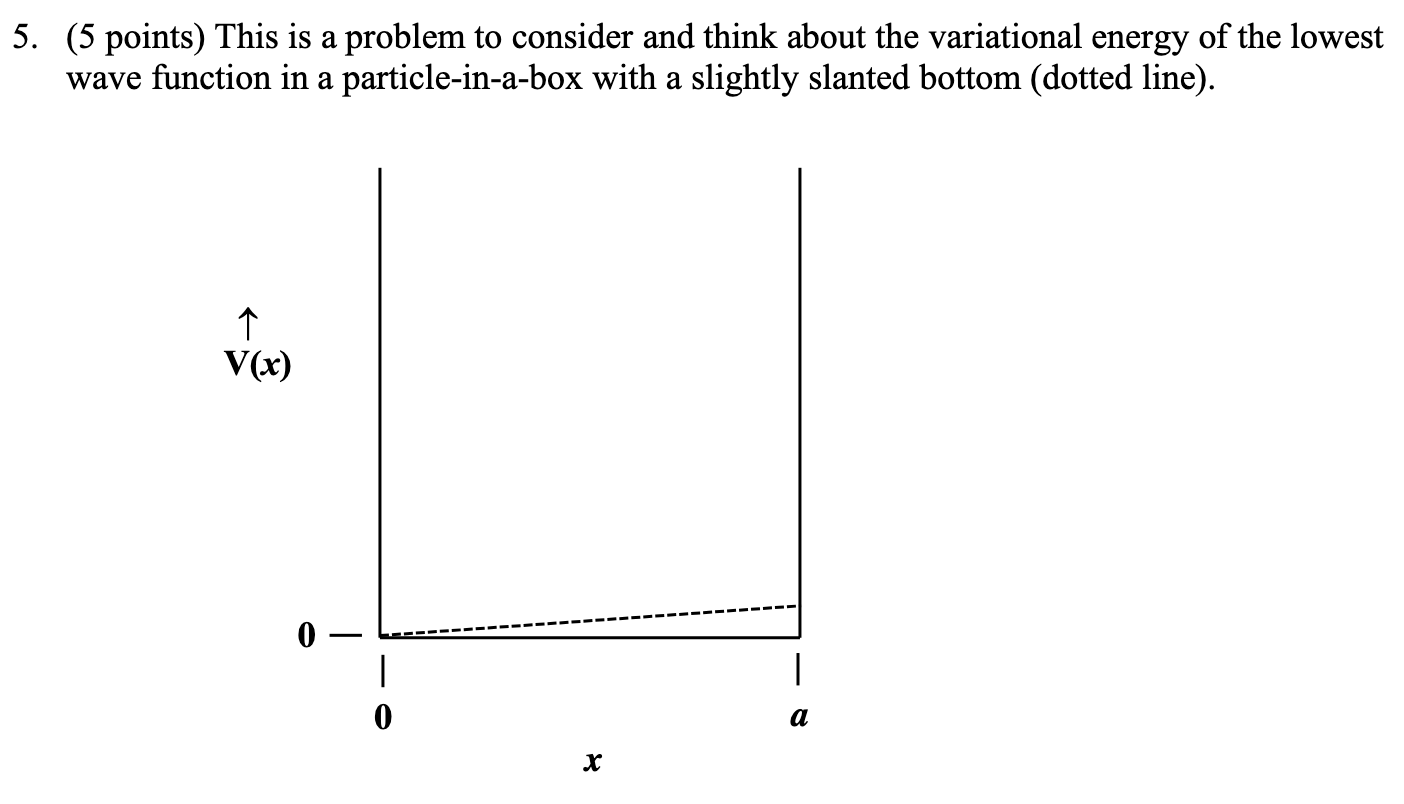
5. (5 points) This is a problem to consider and think about the variational energy of the lowest wave function in a particle-in-a-box with a slightly slanted bottom (dotted line). V(x) x | a Assume the lowest wave function is: trial TTX = sin + sin 2 where is the variational , a a parameter. These are the n = 1 and n = 2 particle-in-a-box wave functions. The slanted portion has a potential given by V(x) = where k is a small energy. kx a (c) Write out the Hamiltonian for this particle-in-a-box. (d) Write out the variational principle integrals in detail for the expectation value of the energy . Don't forget the normalization of the wave function and to put in the proper limits of integration. Do not solve the integrals. (e) If you had solved the integrals, discuss what has to be done next to minimize the energy E. (f) Now think physically what the value of might be. Is it positive or negative? Why? Is it small or large? Why? Show in pictures. Show the old energies and wave functions for n = = 1 and n = 2 and the new energy and new wave function for the slanted bottom.