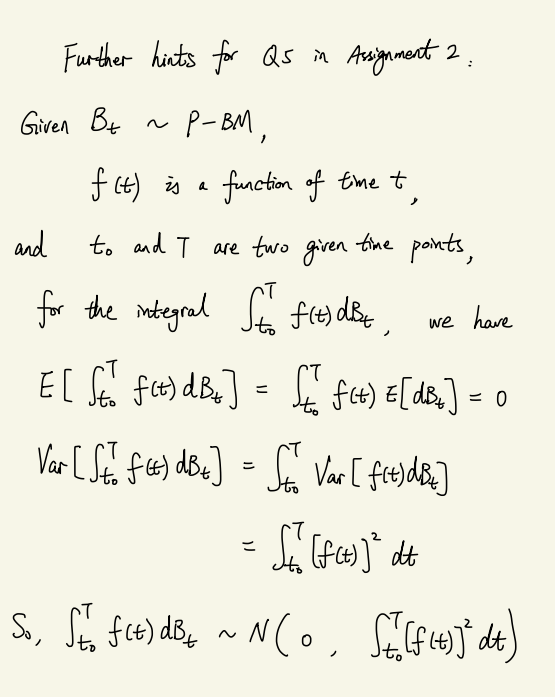
5. Brownian Motion, Ito's Lemma and Distribution The Ornstein-Uhlenbeck or mean reverting process can be useful for modeling a time series whose value changes stochastically but which tends to revert to a long-run value (its unconditional or steady state mean). This continuous-time process is given by dy(t)=[a-By(t)]dt +dz(t) where dz(t) is a standard Brownian motion under P-measure. The process is sometimes referred to as an elastic random walk. y(t) varies stochastically around its unconditional mean of a/, and is a measure of the strength of the variable's reversion to this mean. Find the distribution of y(t) given y(t), where >to. In particular, find E[y(t) y(t)] and var[y(t) y(to)]. Hint: make the change in variables: x(t) e(-) and apply It's lemma to find the stochastic process for x(t). The distribution and first two moments of x(t) should be obvious. From this, derive the distribution and moments of y(t). Further hints for Qs in Assignment 2 Given Bt ~ P-BM, f (t) is a function of time t , and T to and I are two given time points, T for the integral for fre) dist - we have E[ St. f(t) dB+] = { f(t) =[dB] = 0 Var [Stof (t) dB =] = from Var [f(t) dBz] = {{{[fa] dt So, St f(t) dB ~ N(o, Sc[[f(t)]" dt)