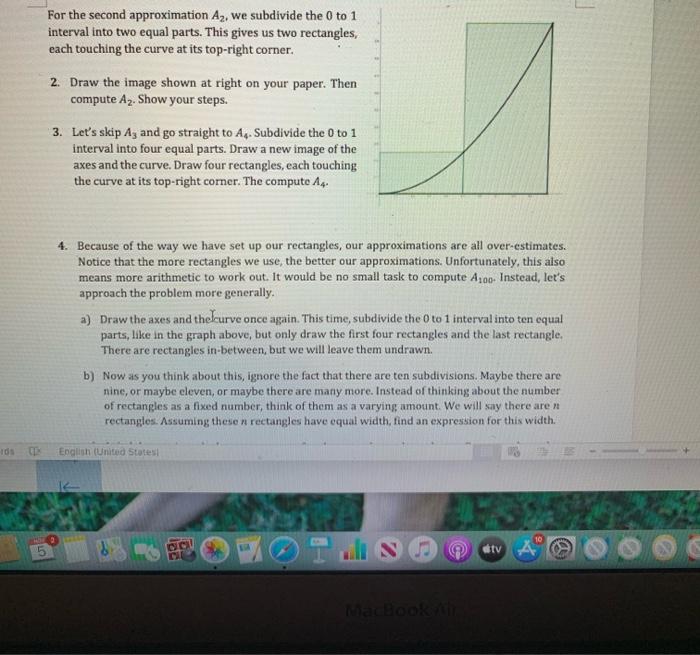
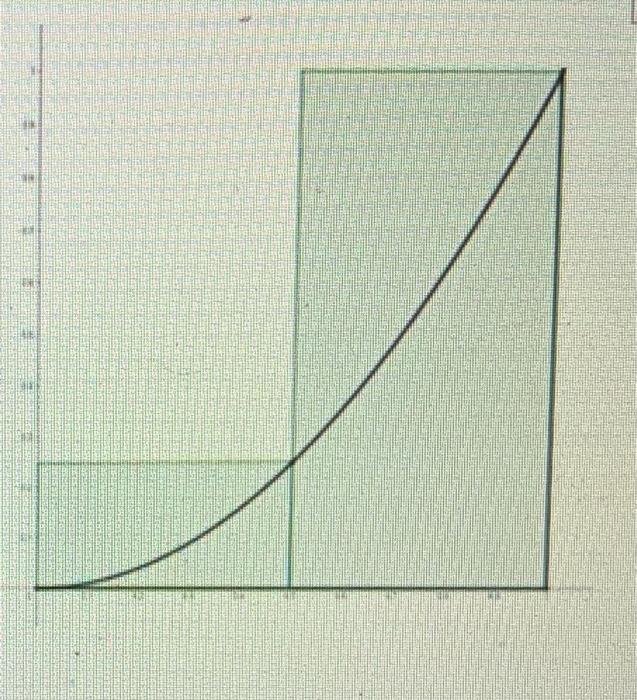
5. Building on the work from exercise 4, we can formulate A,, an approximation of the region based on n rectangles. a) Find an expression for the height of each rectangle you have drawn. b) Find an expression for the area of each rectangle you have drawn. c) Find an expression for A,, by adding up the areas of all the rectangles, even those in-between rectangles you did not draw. You may use an ellipsis (...) to account for the areas of the missing rectangles. 4. Because of the way we have set up our rectangles, our approximations are all over-estimates. Notice that the more rectangles we use, the better our approximations. Unfortunately, this also means more arithmetic to work out. It would be no small task to compute A100. Instead, let's approach the problem more generally. a) Draw the axes and the curve once again. This time, subdivide the 0 to 1 interval into ten equal parts, like in the graph above, but only draw the first four rectangles and the last rectangle. There are rectangles in-between, but we will leave them undrawn. b) Now as you think about this, ignore the fact that there are ten subdivisions. Maybe there are nine, or maybe eleven, or maybe there are many more. Instead of thinking about the number of rectangles as a fixed number, think of them as a varying amount. We will say there are n rectangles. Assuming these n rectangles have equal width, find an expression for this width c) Label the x-axis at the bottom corners of each rectangle you have drawn. For example, at the bottom-left corner of the first rectangle is zero. That one is easy. 5. Building on the work from exercise 4, we can formulate An, an approximation of the region based on n rectangles. a) Find an expression to the height of each rectangle you have drawn. b) Find an expression for the area of each rectangle you have drawn. c) Find an expression for A, by adding up the areas of all the rectangles, even those in-between rectangles you did not draw. You may use an ellipsis (..) to account for the areas of the missing rectangles. For the second approximation Az, we subdivide the 0 to 1 interval into two equal parts. This gives us two rectangles, each touching the curve at its top-right corner. 2. Draw the image shown at right on your paper. Then compute Az. Show your steps. 3. Let's skip Az and go straight to A Subdivide the 0 to 1 interval into four equal parts. Draw a new image of the axes and the curve. Draw four rectangles, each touching the curve at its top-right corner. The compute As. 4. Because of the way we have set up our rectangles, our approximations are all over-estimates. Notice that the more rectangles we use the better our approximations. Unfortunately, this also means more arithmetic to work out. It would be no small task to compute A300. Instead, let's approach the problem more generally. a) Draw the axes and the curve once again. This time, subdivide the 0 to 1 interval into ten equal parts, like in the graph above, but only draw the first four rectangles and the last rectangle There are rectangles in-between, but we will leave them undrawn. b) Now as you think about this, ignore the fact that there are ten subdivisions. Maybe there are nine, or maybe eleven, or maybe there are many more. Instead of thinking about the number of rectangles as a fixed number, think of them as a varying amount. We will say there are rectangles. Assuming these n rectangles have equal width, find an expression for this width. English (United States dtv