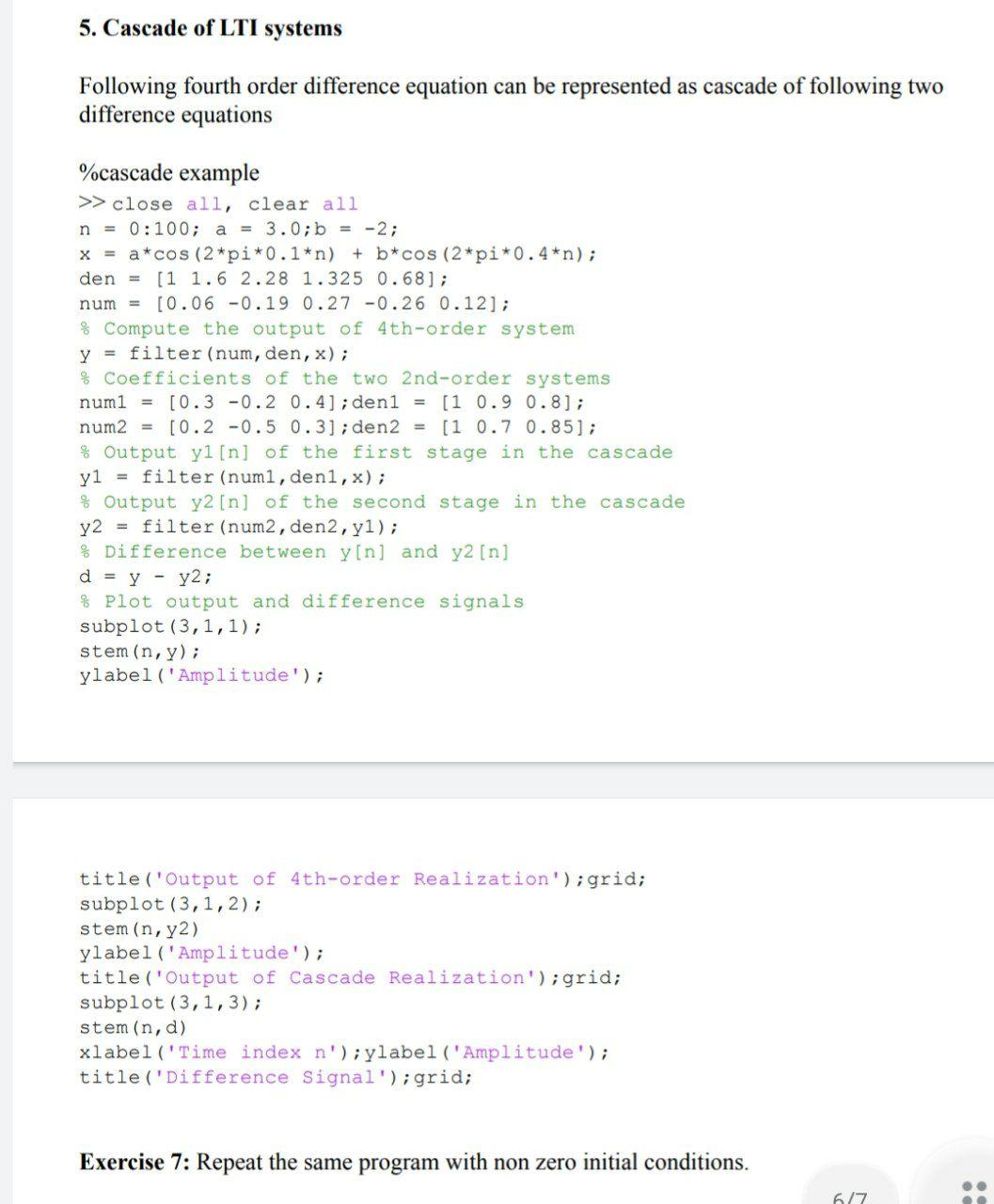
5. Cascade of LTI systems Following fourth order difference equation can be represented as cascade of following two difference equations %cascade example >> close all, clear all n = 0:100; a = 3.0;b = -2; x = a*cos (2*pi*0.1*n) + b*cos (2*pi*0.4*n); den = [1 1.6 2.28 1.325 0.68]; num = [0.06 -0.19 0.27 -0.26 0.12]; Compute the output of 4th-order system y = filter (num, den, x); % Coefficients of the two 2nd-order systems num1 = [0.3 -0.2 0.4]; den1 = [1 0.9 0.8]; num2= [0.2 -0.5 0.3]; den2 = [1 0.7 0.85]; % Output y1 [n] of the first stage in the cascade yl filter (numl, den1, x); % Output y2 [n] of the second stage in the cascade y2 filter (num2, den2, y1); %Difference between y[n] and y2 [n]. d = y - y2; Plot output and difference signals subplot (3,1,1); stem (n, y); ylabel ('Amplitude'); title ('Output of 4th-order Realization'); grid; subplot (3, 1, 2); stem (n, y2) ylabel ('Amplitude'); title ('Output of Cascade Realization'); grid; subplot (3,1,3); stem (n, d) xlabel('Time index n');ylabel ('Amplitude'); title ('Difference Signal'); grid; Exercise 7: Repeat the same program with non zero initial conditions. 6/7