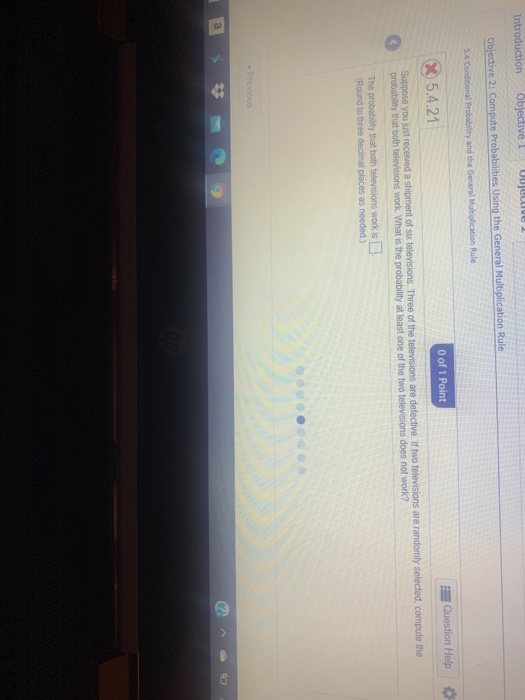
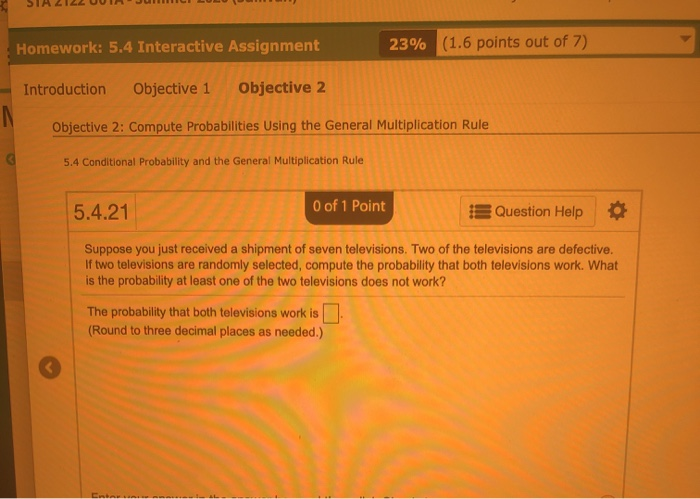
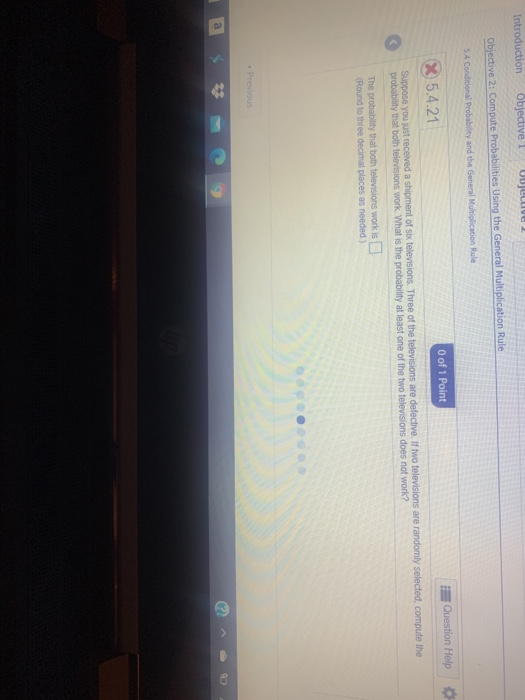
Question
5. On each of four days next week (Monday thru Thursday), Earl will shoot six free throws. Assume that Earl's shots satisfy the assumptions of
5. On each of four days next week (Monday thru
Thursday), Earl will shoot six free throws. Assume that Earl's shots satisfy the assumptions
of Bernoulli trials with p = 0.37.
(a) Compute the probability that on any particular day Earl obtains exactly two successes. For future reference, if Earl obtains exactly two successes on any particular day, then we say that the event "Brad"
has occurred.
(b) Refer to part (a). Compute the probability
that: next week Brad will occur on Monday and Thursday and will not occur on
Tuesday and Wednesday. (Note: You are
being asked to compute one probability.)
16. On each of four days next week (Monday thru
Thursday), Dan will shoot five free throws. Assume that Dan's shots satisfy the assumptions
of Bernoulli trials with p = 0.74.
(a) Compute the probability that on any particular day Dan obtains exactly three successes. For future reference, if Dan obtains exactly three successes on any particular day, then we say that the event "Mel"
has occurred.
(b) Refer to part (a). Compute the probability that: next week Mel will occur exactly
once and that one occurrence will be on
Monday. (Note: You are being asked to
compute one probability.)
17. Alex and Bruce each perform 200 dichotomous
trials. A success is the desirable outcome; it requires more skill than does a failure. You are
given the following information.
? Each of the men achieves exactly 90 successes.
? Alex exhibited evidence of improving
skill over time; and Bruce exhibited evidence of declining skill over time.
25. Bert computes a 95% confidence interval for p
and obtains the interval [0.600, 0.700]. Note:
Parts (a) and (b) are not connected: Part (b) can
be answered even if one does not know how to
do part (a).
(a) Bert's boss says, "Give me a 90% confidence interval for p." Calculate the answer
for Bert.
(b) Bert's boss says, "Give me a 95% confidence interval for p?q." Calculate the answer for Bert. (Hint: p?q = p?(1?p) =
2p ? 1. Bert's interval says, in part, that
"p is at least 0.600;" what does this tell us
about 2p ? 1?)
26. Maggie computes a 95% confidence interval for
p and obtains the interval [0.50, 0.75]. Note:
Parts (a) and (b) are not connected: Part (b) can
be answered even if one does not know how to
do part (a).
(a) Maggie's boss says, "Give me a 95% confidence interval for p
2
." Calculate the answer for Maggie. (Hint: The interval says,
in part, that "p is at most 0.75;" what does
this tell us about p
2
?)
(b) Maggie's boss says, "Give me a 95% confidence interval for p ? q." Calculate the
answer for Maggie. (Hint: p ? q = p ?
(1 ? p) = 2p ? 1. The interval says, in
part, that "p is at most 0.75;" what does
this tell us about 2p ? 1?)


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


