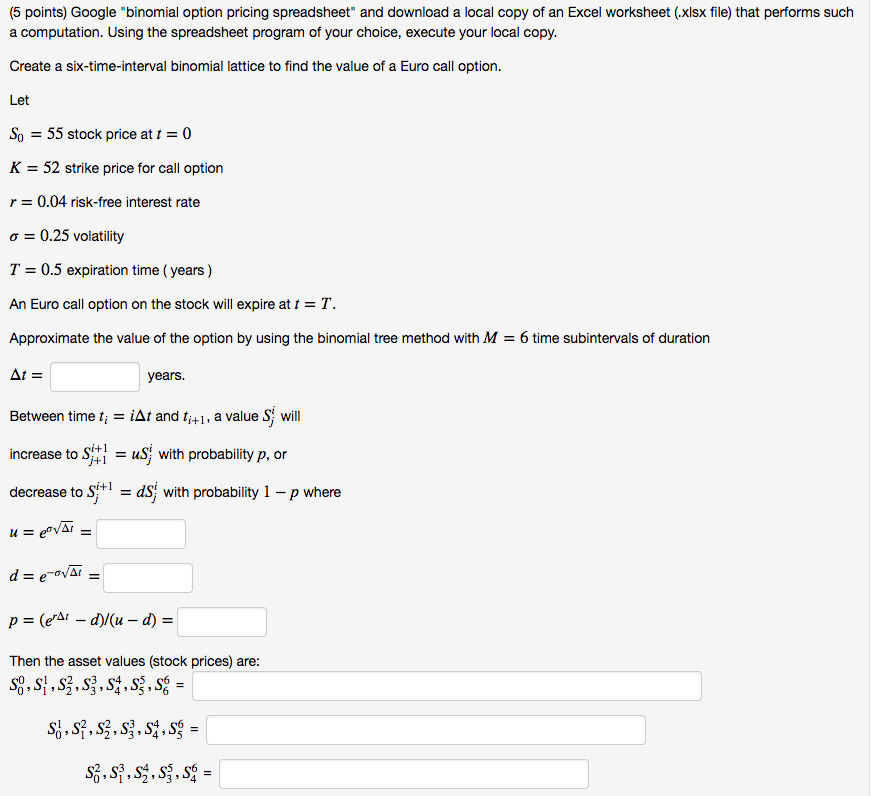
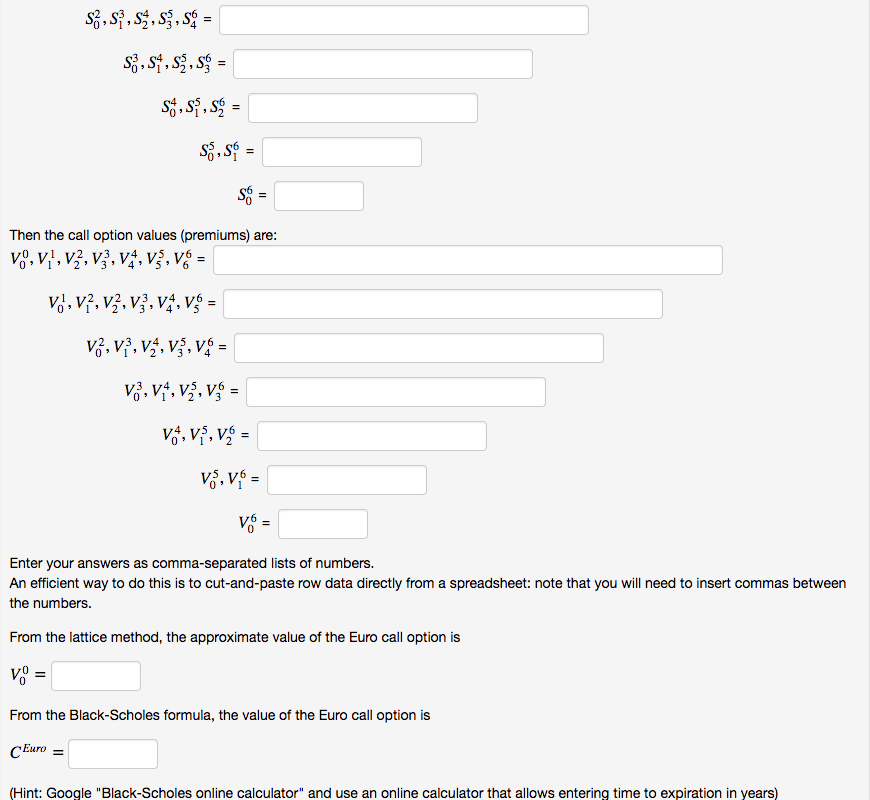
(5 points) Google "binomial option pricing spreadsheet" and download a local copy of an Excel worksheet (.xlsx file) that performs such a computation. Using the spreadsheet program of your choice, execute your local copy. Create a six-time-interval binomial lattice to find the value of a Euro call option Let So 55 stock price at t 0 K 52 strike price for call option r 0.04 risk-free interest rate -0.25 volatility T = 0.5 expiration time ( years ) An Euro call option on the stock will expire at t T. Approximate the value of the option by using the binomial tree method with M 6 time subintervals of duration years. Between time tiAt and t+,a value S will increase to sti-uS with probability p, or decrease to s+ ds with probability 1 - p where Then the asset values (stock prices) are 0123' 4956 0123 495 0 Then the call option values (premiums) are V3.vt,V3.vg. .vf = 0 Enter your answers as comma-separated lists of numbers. An efficient way to do this is to cut-and-paste row data directly from a spreadsheet: note that you will need to insert commas between the numbers From the lattice method, the approximate value of the Euro call option is From the Black-Scholes formula, the value of the Euro call option is Euro Hint: Google "Black-Scholes online calculator" and use an online calculator that allows entering time to expiration in years) (5 points) Google "binomial option pricing spreadsheet" and download a local copy of an Excel worksheet (.xlsx file) that performs such a computation. Using the spreadsheet program of your choice, execute your local copy. Create a six-time-interval binomial lattice to find the value of a Euro call option Let So 55 stock price at t 0 K 52 strike price for call option r 0.04 risk-free interest rate -0.25 volatility T = 0.5 expiration time ( years ) An Euro call option on the stock will expire at t T. Approximate the value of the option by using the binomial tree method with M 6 time subintervals of duration years. Between time tiAt and t+,a value S will increase to sti-uS with probability p, or decrease to s+ ds with probability 1 - p where Then the asset values (stock prices) are 0123' 4956 0123 495 0 Then the call option values (premiums) are V3.vt,V3.vg. .vf = 0 Enter your answers as comma-separated lists of numbers. An efficient way to do this is to cut-and-paste row data directly from a spreadsheet: note that you will need to insert commas between the numbers From the lattice method, the approximate value of the Euro call option is From the Black-Scholes formula, the value of the Euro call option is Euro Hint: Google "Black-Scholes online calculator" and use an online calculator that allows entering time to expiration in years)








