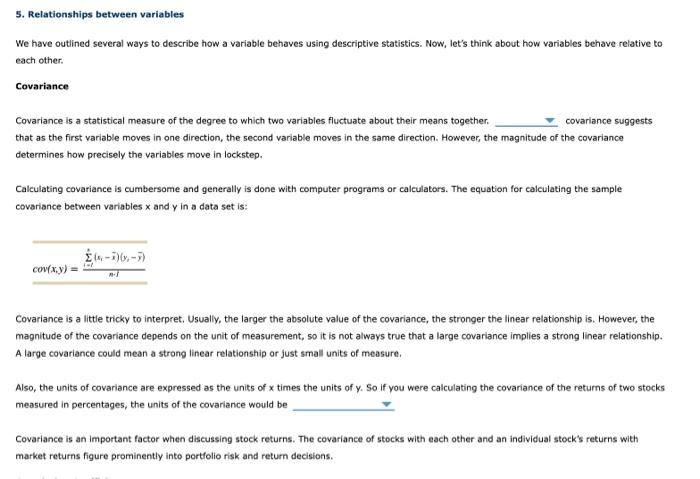
5. Relationships between variables We have outlined several ways to describe how a variable behaves using descriptive statistics. Now, let's think about how variables behave relative to each other. Covariance Covariance is a statistical measure of the degree to which two variables fluctuate about their means together. covariance suggests that as the first variable moves in one direction, the second variable moves in the same direction. However, the magnitude of the covariance determines how precisely the variables move in lockstep. Calculating covariance is cumbersome and generally is done with computer programs or calculators. The equation for calculating the sample covariance between variables x and y in a data set is: cov(x,y)=nfi=ii(six)(yjy) Covariance is a little tricky to interpret. Usually, the larger the absolute value of the covariance, the stronger the linear relationship is. However, the magnitude of the covariance depends on the unit of measurement, so it is not always true that a large covariance implies a strong linear relationship. A large covariance could mean a strong linear relationship or just small units of measure, Also, the units of covariance are expressed as the units of x times the units of y. So if you were calculating the covariance of the returns of two stocks measured in percentages, the units of the covariance would be Covariance is an important factor when discussing stock returns. The covariance of stocks with each other and an individual stock's returns with market returns figure prominently into portfolio risk and return decisions. Covariance is a little tricky to interpret. Usually, the larger the absolute value of the covariance, the stronger the linear relationship is. However, the magnitude of the covariance depends on the unit of measurement, so it is not always true that a large covariance implies a strong linear relationship. A large covariance could mean a strong linear relationship or just small units of measure. Also, the units of covariance are expressed as the units of x times the units of y. So if you were calculating the covariance of the returns of two stocks measured in percentages, the units of the covariance would be Covariance is an important factor when discussing stock returns. The covariance of stocks with each other and an individual stock's returns with market returns figure prominently into portfolio risk and return decisions. Correlation Coefficient The correlation coefficient ( r ) standardizes the tinear relationship (covariance) between two variables and is calculated as: rxy=asdycov(xiy The correlation coefficient overcomes the scaling problem of the covariance. The correlation between any two random variables must satisfy the following equation: 1r1 If the variables are said to be uncorrelated, which of the variables are independent of each other. There are no definitive rules indicating what constitutes weak or strong correlation, but generally a correlation coefficient with an absolute value between 0 and 0.3 is thought to have a weak correlation. Correlation coefficients with an absolute value between 0.3 and 0.6 are moderately correlated, and correlation coefficients with an absolute value higher than 0.6 are strongly correlated. However, it is very important to recognize that correlation does not indicate causality. Just because two variables are highly correlated, that does not mean that either variable causes the other. Correlation merely categorizes the behavior of variables relative to each other; it makes no assertion as to what causes that behavior